HyperMath

MultiRegress

MultiRegress

 Previous topic Next topic No expanding text in this topic  

MultiRegress

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

Linear regression in multiple variables using least squares.  The general form of the equation for the fit is:

multiregImg1

where xi represents an independent variable whose values are sampled.  Each fi is a known function operating on an independent variable.  And y is the dependant variable whose values are also sampled.  Each ai represents the coefficient that is to be determined.

The problem is cast in the form:

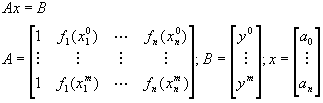
multiregImg2

where the superscript represents each instance of the total sample m.  The system is solved for the vector x in a least squares sense.

Syntax

Coeff, R, Corr = MultiRegress(A, B)

Arguments

Name

Description

 

A

A matrix of regression data as defined above.  Its number of rows are the same as the number of samples and the number of columns same as the number of independent variables.  Note that the first column of one's is to accommodate the constant term but is not enforced.

 

B

The right-hand side column vector or a matrix.  If it is a matrix, each column is considered a separate vector and the system is solved separately for each, resulting in multiple solutions.  The number of rows must be equal to the number of rows of matrix A.

Output

Name

Description

 

Coeff

A vector of the coefficients that best fit the equation to the data in a least squares sense. It will have the same number of rows as the number of columns of A and same number of columns as B.  Each column will be a solution corresponding to the equivalent column in B.

 

R

A scalar or vector of mean squared errors.  One value for each column of B.

 

Corr

A scalar or vector of correlations.  One value for each column of B.

Example

Given m samples of two independent variables x and y and a dependant variable z, find the best fit to the sampled data with the equation:

z = a0 + a1x + a2y2 (that is f1(x)= x & f2(x)= x2)

Create an mX3 matrix of regression data as follows:

multiregImg3

Then create an mx1 column vector of the sampled data of the dependent variable z as follows:

multiregImg4

 

Syntax

 

Coeff, R, Corr = MultiRegress(A, B)

 

Result

 

Coeff is a 3x1 vector of the coefficients ao, a1, and a2.

R will be a scalar of the mean squared error.

Corr will be a scalar of the correlation.

See Also:

ExpFit

NLCurveFit