|
»Click here to display Table of Contents«
|
Hammersley |
|
|
|
|
|
Hammersley |
|
|
|
|
|
»Click here to display Table of Contents«
|
Hammersley |
|
|
|
|
|
Hammersley |
|
|
|
|
Hammersley sampling belongs to the category of quasi-Monte Carlo methods. This method uses a quasi-random number generator, based on the Hammersley points, to uniformly sample a unit hypercube.
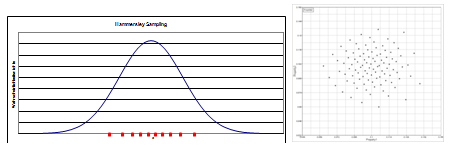
Figure 1: Illustration of Hammersley Sampling
Hammersley sampling generates the 
input variable values for 
designs as:
where 
is the number of designs, 
is the number of variables, 
is the design index (in our case starting from 0), 
are the first n-1 prime numbers (2,3,5,7…) and 
are calculated as:
where 
are the coefficients of integer, 
in radix-R notation which is represented as:
where
| • | Hammersley sampling is an efficient sampling method that provides reliable estimates of output statistics using fewer samples than random sampling. |
| • | A correlation structure can be specified to reflect the correlation existing between random variables. Applying a correlation structure can be costly for a large number of input variables. |
In the Specifications step, you can change the following setting of Hammersley from the Settings tab.
Parameter |
Default |
Range |
Description |
Number of runs(npt) |
100 |
> 0 |
Number of designs to be evaluated. |
Apply User Correlations |
true |
true or false |
Apply user specified correlations on the data. |