Least Squares Regression

Least Squares Regression (LSR) method creates a regression polynomial of the chosen order such that the sum of the squares of the differences (residuals) between output response values predicted by the regression model and the corresponding simulation model is minimized; for example:

where n is the number of designs, f predicted is the output response value predicted by the regression model for the ith design, and f is the output response value from the simulation of the ith design. This is achieved by finding the regression model coefficient values that sets the derivative of E, with respect to each unknown coefficient, to zero.

Usability Characteristics

•	HyperStudy will create the least squares regression of any order, however, in most cases polynomials of the 4th order or higher do not increase accuracy.

•	A custom order can be defined from the Regression Terms tab. Before a custom order can be defined you must set Regression Model to Custom from the Settings in the Specification tab.

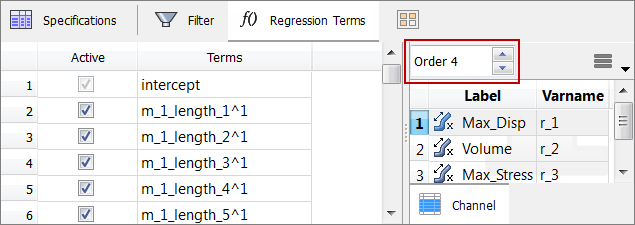
lsr_custom_order

Defining custom order in the Regression Terms tab.

•	Suppress regression terms that are known to be insignificant by clearing their corresponding checkboxes in the Active column of the Regression Terms tab.

In order to suppress regression terms you must set Regression Model to Custom from the Settings in the Specification tab.

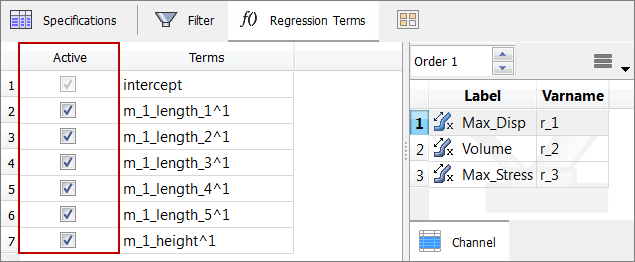
regression_terms

•	Residuals and diagnostics should be used to gain an understanding of the quality of the fit.

•	Quality of a LSR fit is a function of the number of runs, order of the polynomial, and the behavior of the application.

•	If the residuals and diagnostics are not good for a LSR fit, than you can increase the order of the Fit provided you have enough runs to fit that specific order.

Note:

If n is the number of input variables:

-	A linear model requires n + 1 runs.

-	An interaction model requires runs.

-	A quadratic model requires runs.

•	If increasing the order does not improve the fit quality, then you may want to inspect the input matrix collinearity and optionally add more runs. You should try the other available Fit methods as your application may have more non-linearity than polynomials can handle.

Settings

In the Specifications step, you can change the settings of LSR from the Settings tab.

Note:

Order is a critical setting for the quality of Fit. If the Fit diagnostics are poor, then it is advised that you increase the Order to include more terms in the regression, provided that you have a high enough number of runs to create that approximation.

In the Settings tab, you can access the following settings:

Parameter

Default

Range

Description

Regression Model

Linear

Squared

Cubic

Interaction

Full Quadratic

Full Cubic

Custom

Linear

First order terms only.

y=A+Bx+Cy

Squared

Second order without cross terms.

y=A+Bx+Cy+Dx^2+Ey^2

Cubic

Third order without cross terms.

y=A+Bx+Cy+Dx^2+Ey^2+Fx^3+Gy^3

Interaction

Linear and the cross terms.

y=A+Bx+Cy+Dxy

Full Quadratic

Complete second order polynomial.

Full Cubic

Complete third order polynomial.

Custom

User defined order and terms.