Composite Material

In RADIOSS the following material laws are used to describe composite material:

•	LAW12 and LAW14

•	LAW15 (recommended to use LAW25+/FAIL/CHANG)

•

LAW25

•	LAW19 (For Fabric and with only /PROP/TYPE9)

•	LAW58 (For Fabric only with /PROP/TYPE16)

Table 1: Composite material, property, failure model, and element type compatibility

	Shell Element	Brick Element	Failure Model
LAW12		/PROP/TYPE6 (SOL_ORTH) /PROP/TYPE21 (TSH_ORTH) /PROP/TYPE22 (TSH_COMP)	/FAIL/HASHIN /FAIL/PUCK /FAIL/LAD_DAMA
LAW14		/PROP/TYPE6 (SOL_ORTH) /PROP/TYPE21 (TSH_ORTH) /PROP/TYPE22 TSH_COMP)	/FAIL/HASHIN /FAIL/PUCK /FAIL/LAD_DAMA
LAW15	/PROP/TYPE9 (SH_ORTH) /PROP/TYPE10 (SH_ORTH) /PROP/TYPE11 (SH_SANDW) /PROP/TYPE17 (STACK) /PROP/TYPE19 (PLY)		/FAIL/CHANG
LAW25	/PROP/TYPE10 (SH_ORTH) /PROP/TYPE11 (SH_SANDW) /PROP/TYPE17 (STACK) /PROP/TYPE19 (PLY) /PROP/TYPE51	/PROP/TYPE6 (SOL_ORTH) /PROP/TYPE14 (SOLID) /PROP/TYPE20 (TSHELL) /PROP/TYPE21 (TSH_ORTH) /PROP/TYPE22 TSH_COMP)	/FAIL/CHANG /FAIL/HASHIN /FAIL/PUCK /FAIL/LAD_DAMA (for solid only)
LAW19	/PROP/TYPE9 (SH_ORTH)
LAW58	/PROP/TYPE16 (SH_FABR)

LAW12 and LAW14

LAW12 and LAW14 describe orthotropic solid material which use the Tsai-WU formulation. The materials are 3D orthotropic-elastic, before the Tsai-Wu criterion is reached. LAW12 is a generalization and improvement of LAW14.

Elastic phase

Both material laws require Young's modulus, shear modulus and Poisson ratio (9 parameters) to describe the material orthotropic in elastic phase.

composite_materials_elastic_phase

Stress damage

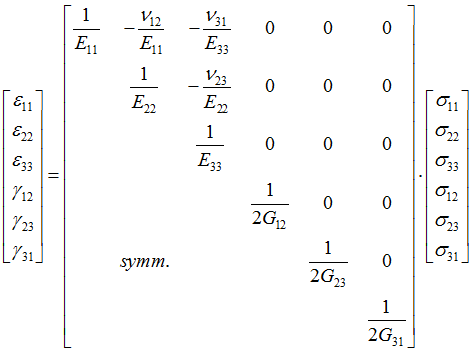
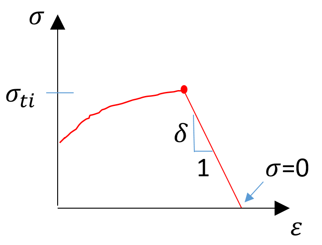
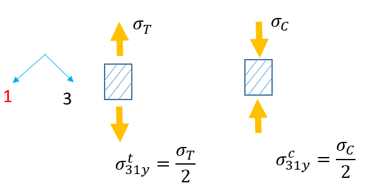
Stress limits (in tensile/compression) are requested for damage. These stress limits could be observed from a tensile test in 3 related directions.

composite_materials_fiber_direction

Once stress limit is reached, then damage to material begins (stress reduced with damage parameter ). If Damage () reaches D=1, then stress is reduced to 0.

composite_materials_stress_limit

Tsai-Wu yield criteria

In LAW12 (3D_COMP), the Tsai-Wu yield criteria is:

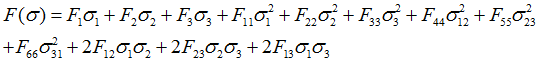
The 12 coefficients of the Tsai-Wu criterion could be determined using the yield stress from the following tests:

Tensile/compression tests

•	Longitude tensile/compression (in direction 1):

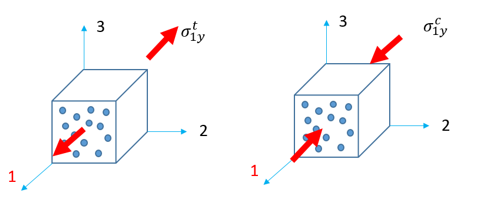
composite_materials_longitude_dir1

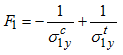
•	Transverse tensile/compression (in direction 2)

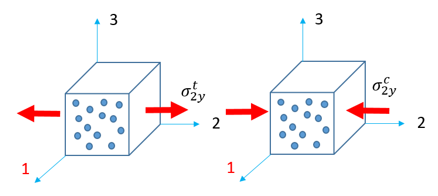
composite_materials_transvers_dir2

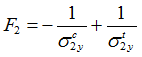
•	Transverse tensile/compression (in direction 3)

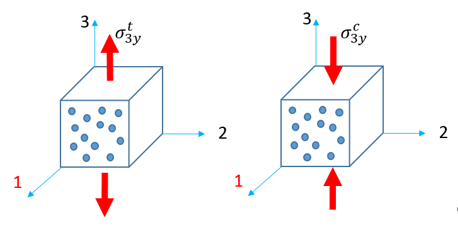
composite_materials_transvers_dir3

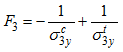
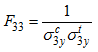
Then the interaction coefficients can be calculated as:

Shear tests

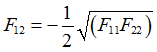
•	Shear in plane 1-2 test:

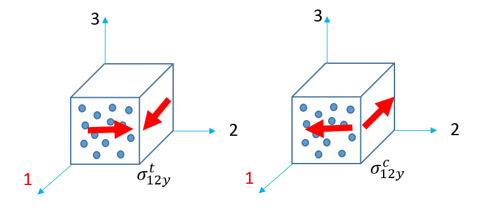
composite_materials_shear_plane1-2

and can result from the sample tests below:

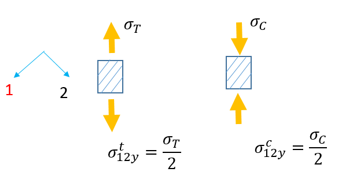
composite_materials_sample_plane1-2

•	Shear in plane 1-3

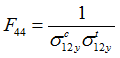
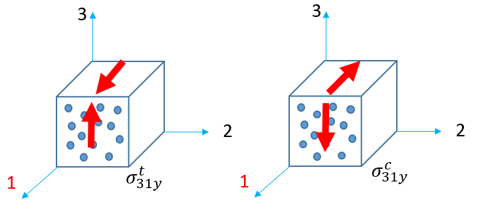
composite_materials_shear_plane1-3

and can result from the sample tests below:

composite_materials_sample_plane1-3

•	Shear in plane 2-3

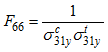
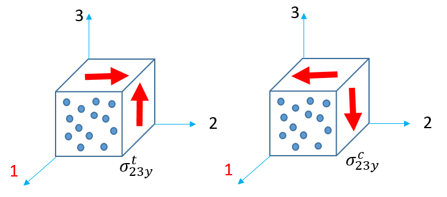
composite_materials_shear_plane2-3

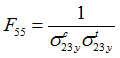
The parameters shown below in LAW12 and LAW14 are requested to calculate the Tsai-Wu criteria:

composite_materials_parameters

The yield surface for Tsai-Wu is . As long as , the material is in the elastic phase. Once , the yield surface is exceeded and the material is in nonlinear phase.

In these two material laws, the following factors could also be considered for yield surface.

•	Plastic work with parameter B and n

•	Strain rate with parameter and c.

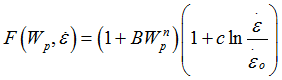
Then the yield surface will be .

•	Material will be in elastic phase, if

•	Material will be in nonlinear phase, if

This yield surface will be limited with (). Where is the maximum value of the Tsai-Wu criterion limit.

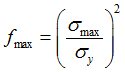
Depending on parameter B, n, c and , the yield surface is between 1 and .

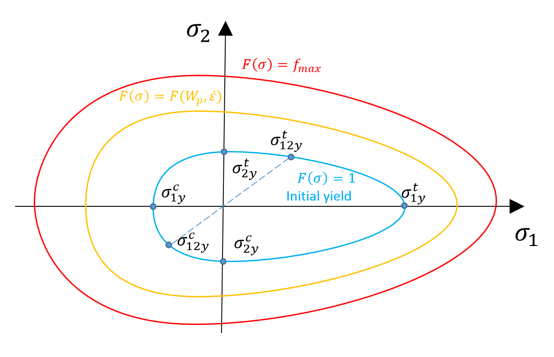
composite_materials_tsai-wu_criteria

Fig1: Tsai-Wu yield criteria in 1-2 plane

LAW25 (Tsai-WU and CRASURV)

LAW25 is the most commonly used composite material in RADIOSS. It can be used with shell and solid elements. The two formulations available in LAW25 are the Tsai-Wu and CRASURV formulations.

Elastic phase

In the elastic phase, Young's modulus (3 parameters), shear modulus (3 parameters) and one parameter for Poisson ratio are required to describe the orthotropic material.

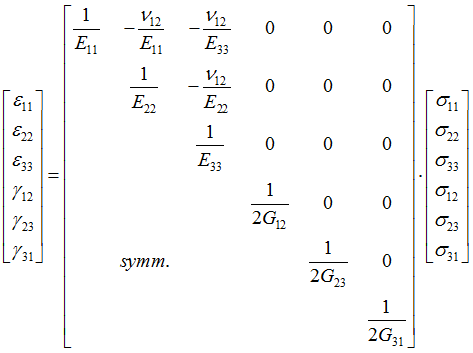
Tsai-Wu yield criteria in LAW25 for Iform=0 and Iform=1

1.	The Tsai-Wu yield surface in LAW25 is defined with 6 coefficient as follows:

	Iform=0: Tsai-Wu	Iform=1: CRASURV
Tsai-Wu yield surface

2.	These 6 coefficients could be determined with yield stress from these tests:

Iform=0: Tsai-Wu

Iform=1: CRASURV

Tensile/compression tests

Longitudinal tensile/compression tests (in direction 1 which is fiber direction):

composite_materials_dir1

In tension:

In compression:

Here

Transverse tensile/compression tests

(in direction 2)

composite_materials_dir2

In tension:

In compression:

Shear tests

Shear in plane 1-2

composite_materials_plane1-2

and can result from the sample tests:

composite_materials_sample_plane1-2

In shear:

can result from the sample test:

composite_materials_shear_crasurv

Interaction coefficients

The default reduction factor, , is typically used.

3.	Note that the relative plastic work is used in Tsai-Wu to calculate the yield surface; whereas in CRASURV, the relative plastic work is used to calculate the yield stress.

Iform=0: Tsai-Wu

Iform=1: CRASURV

Yield surface limit

With

Here

Material in elastic phase, if

Material in nonlinear phase, if composite_materials_tsai-wu_criteria

The yield stress limit is in range of 1 and

Material in elastic phase, if

Material in nonlinear phase, if

composite_materials_crasurve_criteria

4.	In LAW25 (Tsai-Wu and CRASURV) damage is a function of the total strain and the maximum damage factor.

If the total strain or out of plane strain , then the material is softened using the following method:

with i=1,2,3

Where, di is the damage factor and is defined as:

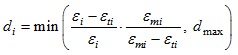with i=1,2

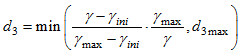in direction 3 (delamination)

•	If the total strain is between , the material begins to soften, but this damage is reversible. Once , then the damage is irreversible and if , then stress in material is reduced to 0.

•	Damage could be in elastic phase or in plastic phase. It depends on which phase and are defined in.

•	Element deletion is controlled by Ioff. Select a different Ioff option to control the criteria of element deletion. For additional information, refer to Ioff in LAW25 in the Reference Guide.

LAW19 and LAW58 for Fabric

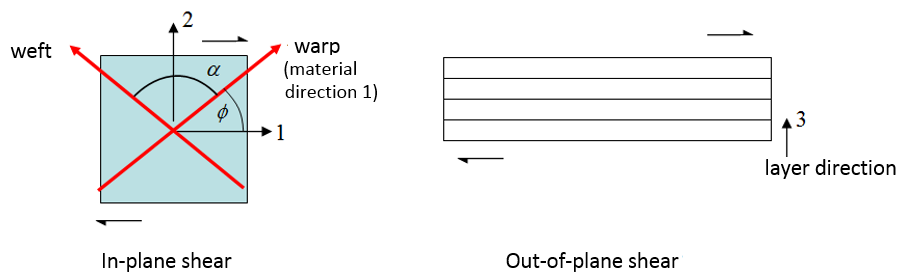
RADIOSS has two material laws for modeling fabrics LAW19 and LAW58. LAW19 is an elastic orthotropic material and must be used with /PROP/TYPE9. LAW58 is hyperelastic anisotropic fabric material and must be used with /PROP/TYPE16. Coupling between warp and weft directions could be defined in this material law to reproduce physical interaction between fibers. Both material laws are often used for airbag modeling.

In LAW58, two methods are provided to define the stress-strain behavior.

•	Nonlinear function (fct_IDi) curve to define the warp, weft and shear behavior

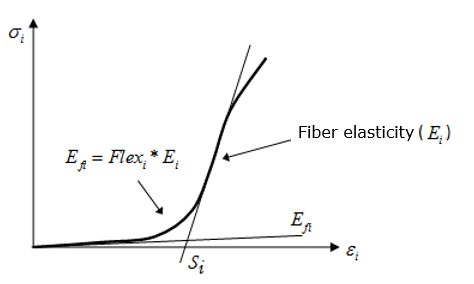
•	Young's modulus, soften coefficient B, straightening strain Si and fiber bending modulus reduction factor Flexi

In warp and weft direction:

if 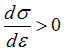(straightening phase)

For in-plane shear in initial state, use G0. Once (angle between wrap and weft) reaches (shear lock angle), then use GT to describe the strengthening.

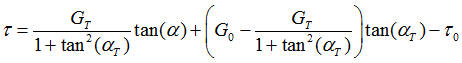
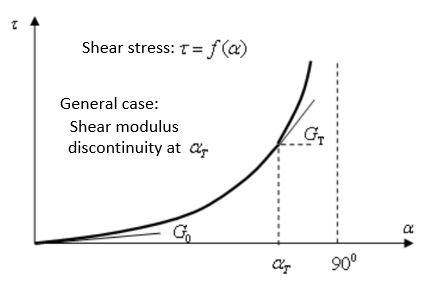
composite_materials_shear_stress

For out-of-plane shear stress-strain is described with Gsh.

composite_materials_stress-strain

For fiber elasticity, if you tensile the fiber, due to the fiber not tighten yet and show very soft.

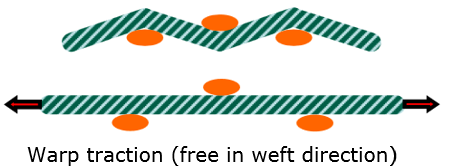
composite_materials_warp_traction

In LAW58, use Flexi to describe this behavior:

Once the strengthening strain Si is reached, then normal fiber elasticity Ei could be used.

composite_materials_fiber_elasticity