Linear pattern grouping allows you to force OptiStruct to create beads in a given direction along the entire length of the part. This can be very useful for optimizing the shape of extruded parts which must maintain a constant cross section. It is also very useful when optimizing the side walls of stamped plates whose beads must run from the top to the bottom so that the part can be drawn from the die. In solid models, where the variable needs to control the movement of all grids through the thickness, linear pattern grouping is also very useful.

For linear pattern grouping (TYP = 1, 21, or 31), OptiStruct generates shape variables that run along a line parallel to the first vector. These shape variables have a width equal to the minimum bead width parameter but have no limit on length. For simple linear pattern grouping, the anchor point and first vector can be located anywhere.

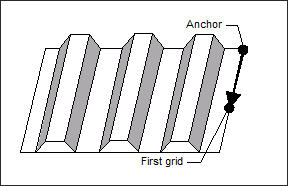
TYP = 1: Linear pattern grouping

For one and two plane linear symmetry, the anchor point locates the plane(s) of symmetry. For one plane linear symmetry (TYP = 21), the second vector defines the symmetry plane (since the first vector has been used to define the direction of the pattern).

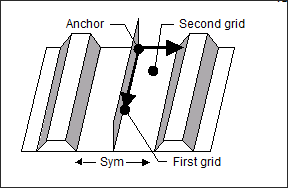
TYP = 21: One plane linear symmetry

For two plane symmetry (TYP = 31), the symmetry planes are defined by the second vector and the cross product of the first and second vectors as shown below. There is no three plane linear pattern grouping since the pattern is automatically symmetric in the direction of the first vector.

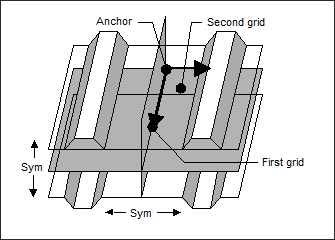
TYP = 31: Two plane linear symmetry