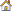HyperStudy

HS-4230: Optimization Study with Discrete Variables

HS-4230: Optimization Study with Discrete Variables

 Previous topic Next topic Expand/collapse all hidden text  

HS-4230: Optimization Study with Discrete Variables

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

In this tutorial you will learn how to use discrete variables. The sample base input template plate.tpl can be found in <hst.zip>/HS-4230/and copied to your working directory.

The objective of this tutorial is to maximize the minimum frequency of the first five modes of a plate. The input variables are the thickness of each of the three components, defined in the input deck via the PSHELL card. The thickness should be between 0.05 and 0.15; the initial thickness within the files is 0.1. The optimization type is size. Furthermore, optimum design should have input variables from a discrete set of 0.05, 0.08, 0.11, and 0.14 for all three thicknesses. By default, HyperStudy will add the values from the lower and upper bounds to this set. Hence the resulting set is 0.05, 0.08, 0.11, 0.14, and 0.15. Delete any of these values if needed.

hs_4225_Double symmetric plate model.

Figure 1: Double Symmetric Plate Model

hmtoggle_plus1greyStep 1: Perform the Study Setup
1.Start HyperStudy.
2.To start a new study, click File > New from the menu bar, or click files_new_hst2 on the toolbar.
3.In the HyperStudy – Add dialog, enter a study name, select a location for the study, and click OK.
4.Go to the Define models step.
5.Add a Parameterized File model.
a.From the Directory, drag-and-drop the plate.tpl file into the work area.

hs_4230_drag_drop_model

b.In the Solver input file column, enter plate.fem. This is the name of the solver input file HyperStudy writes during any evaluation.
c.In the Solver execution script column, select OptiStruct (os).

hs_1020_define_models

6.Click Import Variables. Three input variables are imported from the plate.tpl file.
7.Go to the Define Input Variables step.
8.Click the Details tab.
9.In the Mode column of all three input variables, select Discrete.

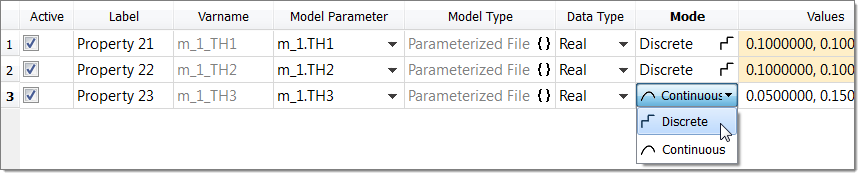
hs_4230_discrete variables

10.In the Values column of Variable 1, click hs_popupdialogicon.
11.Click Step Size, enter 0.03, and click Set.

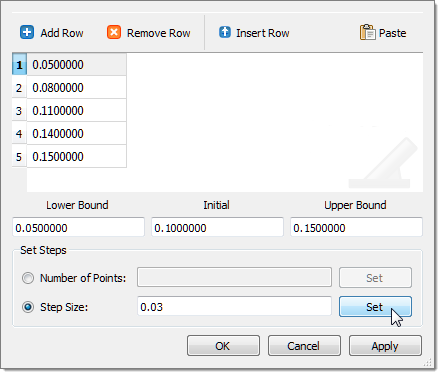
hs_4230_set

12.Click Apply.
13.Click OK.
14.Repeat steps 10 through 13 for Variable 2 and Variable 3.
15.Go to the Specifications step.

 
hmtoggle_plus1greyStep 2: Perform the Nominal Run
1.In the work area, set the Mode to Nominal Run.
2.Click Apply.
3.Go to the Evaluate step.
4.Click Evaluate Tasks. An approaches/nom_1/ directory is created inside the study directory. The approaches/nom_1/run__00001/m_1 sub-directory contains the plate.out file, which is the result of the nominal run, and will be used in the Optimization.
5.Go to the Define Output Responses step.

 
hmtoggle_plus1greyStep 3: Create and Define Output Responses
1.Click Add Output Response.
2.In the HyperStudy - Add dialog, add two output responses and label them Freq1 and Volume.
3.In the Expression column of the output response Freq1, click hs_popupdialogicon.
4.In the Expression Builder, click the File Sources tab.
5.Click Add File Source.
6.In the HyperStudy - Add dialog, add one Solver output file.

solver_output_file

7.In the File column of Vector 1, click hs_popupdialogicon.
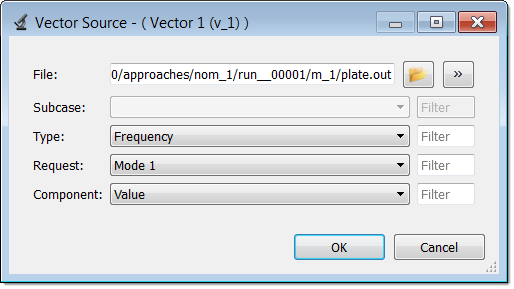
8.In the Vector Source dialog, navigate to the approaches/nom_1/run__00001/m_1 directory and open the plate.out file.
9.Define Vector 1 as the frequency of the plate by selecting the options indicated in the image below from the Type, Request, and Component fields.

hs_4225_vector source

10.Click OK.
11.Click Insert Varname. The expression v_1[0] appears in the Evaluate Expression field.
12.Click OK.
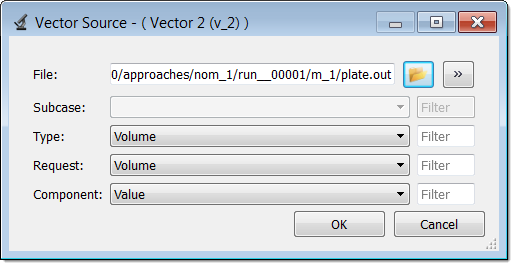
13.Repeat steps 3 through 8 for the output response Volume.
14.Define Vector 2 as the volume of the plate by selecting the options indicated in the image below from the Type, Request, and Component fields.

hs_4230_vector2

15.Click OK.
16.Click Insert Varname. The expression v_2[0] appears in the Evaluate Expression field.
17.Click OK.
18.Click Evaluate Expressions to extract the output response values.

hs_4230_evaluate

 
hmtoggle_plus1greyStep 4: Run an Optimization Study
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Optimization and click OK.
3.Go to the Select Input Variables step.
4.Review the input variable's lower and upper bound ranges.
5.Go to the Select Output Responses step.
6.Click Add Objective.
7.In the HyperStudy - Add dialog, add one objective.
8.Define the objective.
a.Set Type to Minimize.
b.Set Apply On to Volume (r_2).

hs_4230_objectiv e

9.Click the Constraint tab.
10.Click Add Constraint.
11.In the HyperStudy - Add dialog, add one constraint.
12.Define the constraint.
a.Set Apply On to Freq1 (r_1).
b.Set Bound Type to >= (greater than or equal to).
c.For Bound Value, enter 32.

hs_4230_constraint

13.Click Apply.
14.Go to the Specifications step.
15.In the work area, set the Mode to Adaptive Response Surface Method (ARSM).
Note:Only the methods that are valid for the problem formulation are enabled.
16.Click Apply.
17.Go to the Evaluate step.
18.Click Evaluate Tasks.

 
hmtoggle_plus1greyStep 5: View the Iteration History of an Optimization Study
1.Click the Iteration History tab to monitor the progress of the Optimization iteration.

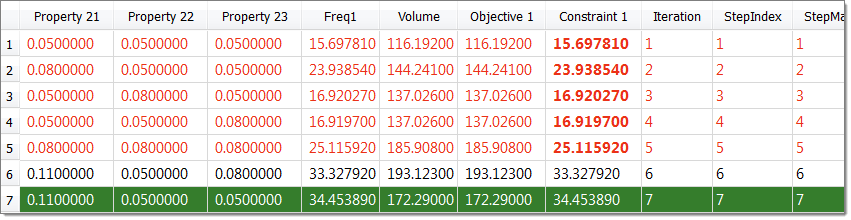
hs_4230_iterationhistory

 
hmtoggle_plus1greyStep 6: Setup a DOE to Find the True Best Design
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Doe and click OK.
3.Go to the Specifications step.
4.In the work area, set the Mode to Full Factorial.
5.Click Apply.
6.Go to the Evaluate step.
7.Click Evaluate Tasks.
8.Go to the Post processing step.
9.Click the Summary tab.
10.Sort run data based on the Volume (which was to be minimized) by right-clicking on the Volume column and selecting Sort down from the context menu. The lowest volume design which satisfies the constraint (frequency > 32) is the same as that found by the optimizer.
Note:The DOE took 125 solver calls to exhaust all combinations, whereas the Optimization found it in 8 solver calls.

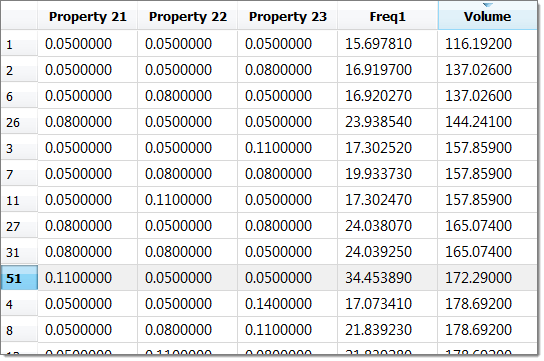
hs_4230_summary_tab

 

 

 

See Also:

HyperStudy Tutorials