HyperStudy

HS-4450: Multi-Objective Optimization of a Cantilever Ibeam using an Inclusion Matrix

HS-4450: Multi-Objective Optimization of a Cantilever Ibeam using an Inclusion Matrix

 Previous topic Next topic Expand/collapse all hidden text  

HS-4450: Multi-Objective Optimization of a Cantilever Ibeam using an Inclusion Matrix

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

The inclusion matrix feature passes an already existing set of data to the running process. In this tutorial, the data created from a DOE is passed to an optimization problem which re-uses the data. This promotes efficient design exploration practices: an optimization using a direct solver call can still be done in combination with a DOE to study the system without any loss of data. This example focuses on the competing objectives in the design of a cantilever ibeam.

The files used in this tutorial can be found in <hst.zip>/HS-4450/.  Copy the files from this directory to your working directory.

hmtoggle_plus1greyStep 1: Perform the Study Setup
1.Start HyperStudy.
2.To start a new study, click File > New from the menu bar, or click files_new_hst2 on the toolbar.
3.In the HyperStudy – Add dialog, enter a study name, select a location for the study, and click OK.
4.Go to the Define models step.
5.Add a Parameterized File model.
a.From the Directory, drag-and-drop the ibeam.tpl file into the work area.

hs_4450_1

b.In the Solver input file column, enter ibeam.py. This is the name of the solver input file HyperStudy writes during any evaluation.
c.In the Solver execution script column, select Python (py).

hs_4450_2

6.Click Import Variables. Four input variables are imported from the ibeam.tpl resource file.
7.Go to the Define Input Variables step.
8.Review the input variable's lower and upper bounds ranges.
9.Go to the Specifications step.

 
hmtoggle_plus1greyStep 2: Perform the Nominal Run
1.In the work area, set the Mode to Nominal Run.
2.Click Apply.
3.Go to the Evaluate step.
4.Click Evaluate Tasks. An approaches/nom_1/ directory is created inside the study directory. The approaches/nom_1/run__00001/m_1 sub-directory contains the output.hstp file, which is the result of the nominal run, and will be used during the Optimization.
5.Go to the Define Output Responses step.

 
hmtoggle_plus1greyStep 3: Create and Define Output Responses
1.Create the Iy output response for the y-axis moment of inertia.
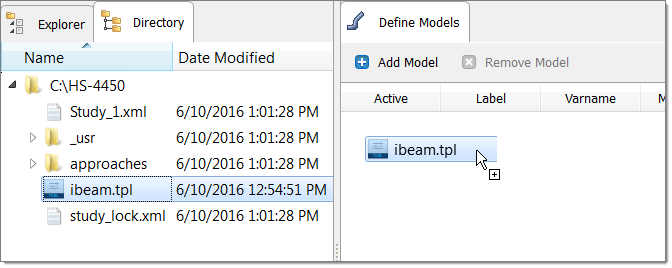
a.From the Directory, drag-and-drop the output.hstp file, located in approaches/nom_1/run_00001/m_1, into the work area.
b.In the File Assistant dialog, set the Reading technology to Altair® HyperWorks® (HstReaderPdd) and click Next.
c.Select Single item in a time series, then click Next.
d.Define the following options, and then click Next.
•Set Type to Output.
•Set Request to Iy.
•Set Component to Value.

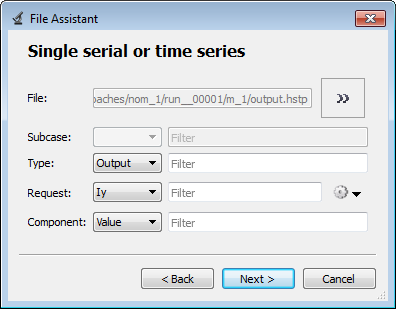
hs_4450_3

e.Label the output response Iy.
f.Set Expression to Maximum.

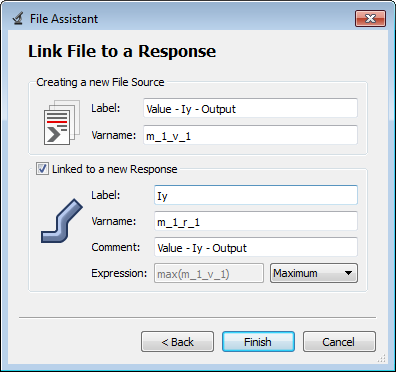
hs_4450_4

g.Click Finish. The Iy output response is added to the work area.
2.Create four more output responses by repeating step 1, except change the component assigned to each output response to the following.

Output Response

Component

Volume

Vol

IZ

Iz

Displacement

d

Frequency1

Freq
3.Click Evaluate Expressions to extract output response values.

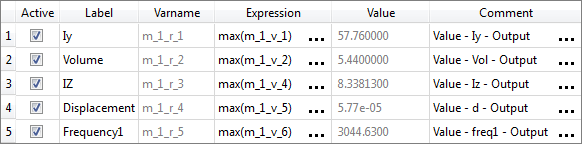
hs_4450_5

4.Click OK. This complete the study setup.

 
hmtoggle_plus1greyStep 4: Run a Hammersley DOE Study
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Doe and click OK.
3.Go to the Specifications step.
4.In the work area, set the Mode to Hammersley.
5.In the Settings tab, verify that the Number of runs is 17.
6.Click Apply.
7.Go to the Evaluate step.
8.Click Evaluate Tasks.
9.Go to the Post processing step, and click the Pareto Plot tab.

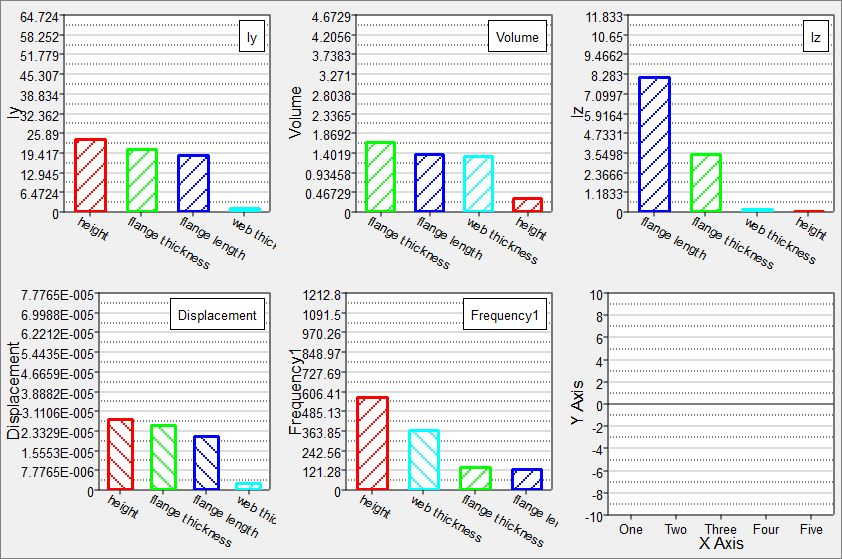
Enable multi-plot and select all of the output responses in the Channel selector. In the options menu, ensure that Effects based on all variables is enabled.

A Pareto Plot shows the ranked influence of the input variables on the output response. For example, for the y-axis moment of the inertia, height has the largest influence and web thickness has the least. In contrast, for the z-axis moment of inertia, the flange length and flange thickness are the most influential variables. The size of the bar indicates the magnitude of the influence, and the hashed line’s slope indicates the sign of the effect: positive or negative. For example, increasing the height will increase Iy, but it will decrease displacement.

hs_4450_10

 
hmtoggle_plus1greyStep 5: Run an Optimization Study
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Optimization and click OK.
3.Go to the Select Input Variables step.
4.Review the input variable's lower and upper bound ranges.
5.Go to the Select Output Responses step.
6.Click Add Objective.
7.In the HyperStudy - Add dialog, add two objectives labeled.
8.Define the two objectives by selecting the options indicated in the image below.

hs_4450_6

9.Click Apply.
10.Go to the Specifications step.
11.In the work area, set the Mode to Global Response Surface Method (GRSM).
Note:Only the methods that are valid for the problem formulation are enabled.
12.Click the More tab and define the following settings:
•Set Points per Iteration to 4.
•Set Use Inclusion Matrix to Without Initial.

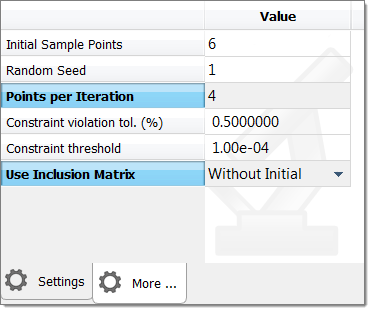
hs_4450_7

13.Import run data from the Doe using an Inclusion Matrix.
a.Click Edit > Inclusion Matrix from the top, right corner of the work area.

hs_4450_8

b.In the Edit Inclusion Matrix dialog, click Import Values.
c.In the Import Values dialog, select Approach Evaluation Data and click Next.
d.Select the approach to Doe 1 and click Next.
e.Click Finish.
f.Review the imported run data and click OK.
14.Click Apply.
15.Go to the Evaluate step.
16.Click Evaluate Tasks to launch the Optimization.
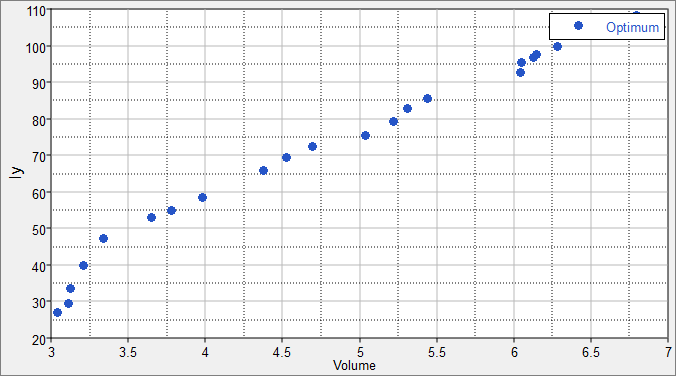
17.Go to the Post Processing step, and click the Optima tab.

Observe the non-dominated front of designs. These points represent the trade-off between the objective of minimizing volume and maximizing the y-axis moment of inertia. In the plot, it is evident that as the moment of inertia increases, the volume increases as well. This curve represents the trade-off of the best available designs given the competing objective requirements.

hs_4450_11

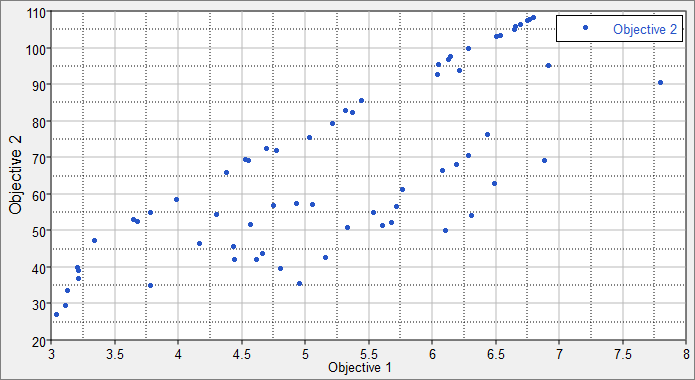
18.Go to the 2D Scatter tab, and plot the objectives along same axes shown in the Optima plot.

This plot shows all of the runs from the optimization. When comparing the scatter and Optima plots, note that the Optima plot contains only the subset of runs which are non-dominated. A dominated design is a design for which both objectives could be improved. A non-dominated design is one in which one objective may only be improved at the expense of another.

hs_4450_12