HyperStudy

Latin Hypercube

Latin Hypercube

 Previous topic Next topic No expanding text in this topic  

Latin Hypercube

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

The Latin Hypercube method, developed by McKay, Conover, and Beckman (1979), is an approach which can yield precise estimates of output statistics with a lesser number of samples than simple random sampling. The Latin Hypercube method uses a constrained or stratified sampling scheme.

Latin Hypercube sampling selects n different values from each of k variables x1, … xk in the following manner:

•The range of each random variable is divided into n non-overlapping intervals on the basis of equal probability.
•One value from each interval is selected at random with respect to the probability density in the interval.
•The n values thus obtained for x1 are paired in a random manner with the n values of x2. These n pairs are combined in a random manner with the n values of x3 to form n triplets and so on, until n k-tuplets are formed.

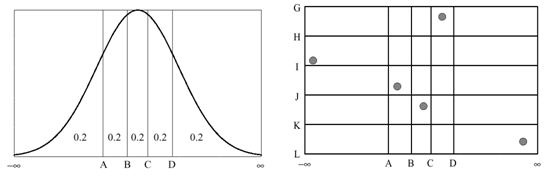
figure_10

Figure 1: Illustration of Latin Hypercube Sampling

Usability Characteristics

•A stratified sampling scheme like Latin Hypercube offers the advantage of selecting random variable values that are uniformly spread across the range of random variables while taking into account the probability density function of those random variables.
•A correlation structure can be specified to reflect the correlation existing between random variables. Applying a correlation structure can be costly for a large number of input variables.

 

Settings

In the Specifications step, you can change the following settings of Latin Hypercube from the Settings tab.

Parameter

Default

Range

Description

Number of runs

(npt)

100

> 0

Number of designs to be evaluated.

Random Seed

(iseed)

1

Integer

0 to 10000

Controlling repeatability of runs depending on the way the sequence of random numbers is generated.

0      random (non-repeatable)

> 0   triggers a new sequence of pseudo-random numbers, repeatable if the same number is specified.

Apply User Correlations

true

true or false

Apply user specified correlations on the data.