Sequential quadratic programming (SQP) is a gradient-based iterative optimization method and is considered to be the best method for nonlinear problems by some theoreticians. In HyperStudy, SQP has been further developed to suit engineering problems.
Usability Characteristics
| • | SQP is a gradient-based method, therefore it will most likely find the local optima. |
| • | One iteration of SQP will require a number of simulations. The number of simulations required is a function of the number of input variables since finite difference method is used for gradient evaluation. As a result, it may be an expensive method for applications with a large number of input variables. |
| • | SQP terminates if one of the conditions below are met: |
| - | One of the two convergence criteria is satisfied. |
| o | “Termination criteria” is based on the Karush-Kuhn-Tucker Conditions (SQPEPS). |
| o | Input variable convergence (DVCONV) |
| - | The maximum number of allowable iterations (MAXDES) is reached. |
| - | An analysis fails and the “Terminate Optimization” option is the default (IGFAIL). |
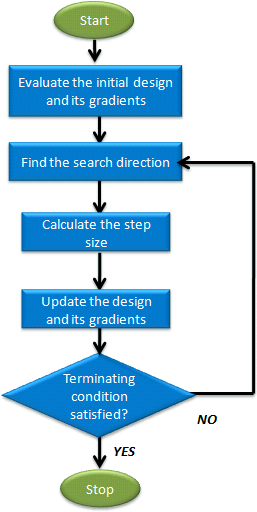
The flowchart below illustrates the different phases of the SQP process.
Settings
In the Specifications step, you can change the settings of SQP from the following tabs:
In the Settings tab, you can access the settings listed below. Please note that for most applications the default settings work optimally, and you may only need to change the Maximum Iterations and On Failed Analysis.
Setting
|
Default Value
|
Range
|
Description
|
Maximum Iterations
(MAXDES)
|
25
|
> 0
|
Maximum number of iterations allowed.
|
Constraint violation tol.
(GMAX)
|
0.1
|
> 0.0
|
Global maximum allowable percentage constraint violation. Constraints must not be violated by more than this value in the converged design.
|
Design var convergence
(DVCONV)
|
0.0
|
>= 0.0
|
Input variable convergence parameter. Design has converged when there are two consecutive designs for which the change in each input variable is less than both (1) DVCONV times the difference between its bounds, and (2) DVCONV times the absolute value of its initial value (simply DVCONV if its initial value is zero). There also must not be any constraint whose allowable violation is exceeded in the last design.
The above description can be formulated as:
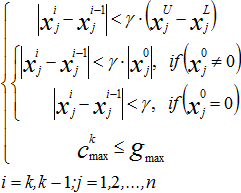
Where,  is input variable; is input variable; 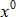 is the initial design; is the initial design; 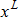 , , 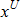 are lower bound and upper bound of input variables respectively; are lower bound and upper bound of input variables respectively; 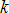 is the current iteration number; is the current iteration number; 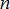 is the number of input variables; is the number of input variables; 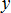 is the input variable convergence parameter. is the input variable convergence parameter.
|
On failed analysis
(IGFAIL)
|
Termination
|
Termination of Ignore Failed Analysis
|
Termination
|
SQP terminates with an error message when an analysis run fails (default).
|
Ignore Failed Analysis
|
SQP ignores the failed analysis run. If analysis is failed at line search then step size is reduced by half and optimization is continued; if analysis is failed at gradient calculation then the corresponding gradient is set to zero (an exception is that if the gradient calculation is failed on all of the input variables, then SQP will be terminated).
|
|
In the More tab, you can access the setting listed below. Please note that for most applications, the default settings work optimally.
Setting
|
Default Value
|
Range
|
Description
|
Termination criteria
(SQPEPS)
|
1.0E-4
|
> 0.0
|
SQP parameter defining the termination criterion, relates to satisfaction of Kuhn-Tucker condition of optimality.
Recommended range: 1.0E-3 to 1.0E-10.
In general, smaller values result in higher solution precision, but more computational effort is needed.
For the nonlinear optimization problem:
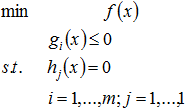
SQP is converged if:
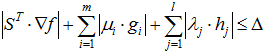
Where s is the search direction generated by SQP; 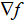 is objective function gradient; is objective function gradient; 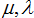 are Lagrange multipliers; are Lagrange multipliers;  is the value of the termination criteria parameter. is the value of the termination criteria parameter.
|
Sensitivity
(DERIV)
|
Forward
FD
|
Forward
FD,
Central
FD,
Asymmetric FD,
Analytical
|
Defines the way the derivatives of output responses with respect to input variables are calculated.
|
Forward FD
|
For approximation by one step forward finite difference scheme.
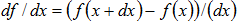
|
Central FD
|
For approximation by two step central (one step forward, one step back) finite difference scheme.
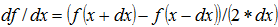
|
Asymmetric FD
|
For approximation by two step non-symmetric (one step forward, half step back) finite difference scheme.
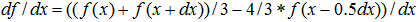
|
For higher solution precision, 2 or 3 can be used, but more computational effort is consumed.
|
Constraint threshold
(EPSCON)
|
1.0e-4
|
> 0.0
|
This parameter is used for constraint value calculation. In general, constraint value is normalized to its bound value. One exception is that, constraint value is not normalized if its absolute bound value is less than this parameter. Recommended range is 1.0e-6 ~ 1.0.
|
Use Perturbation size
(GPTUSE)
|
0
|
0 or 1
|
Enables the use of GPTSIZE, otherwise an internal automatic perturbation size is set.
|
Perturbation size
(GPTSIZE)
|
0.0001
|
> 0.0
|
Defines the size of the finite difference perturbation.
For a variable x, with upper and lower bounds (xu and xl, respectively), the following logic is used to preserve reasonable perturbation sizes across a range of variables magnitudes:
If abs( x) >= 1.0 then perturbation = GPTSIZE * abs( x)
If (xu - xl) < 1.0 then perturbation = GPTSIZE * (xu – xl)
Otherwise perturbation = GPTSIZE
|
Use Inclusion Matrix
(INCLUSI)
|
No
|
No, With Initial, Without Initial
|
| • | No ignores the Inclusion matrix |
| • | With Initial runs the initial point. The best point of the inclusion or the initial point is used as the starting point. |
| • | Without Initial does not run the initial point. The best point of the inclusion is used as the starting point. |
|
|








