Contact |

|

|

|

|
|
Contact |

|

|

|

|
The contact modeling capability for multi-body dynamics can handle complex contact scenarios between rigid bodies and rigid and flexible bodies. For the definition you have to identify geometries on one body that can contact a different set of geometries on a second body. You also specify the contact material properties such as coefficient of restitution and friction. The solver monitors the proximity of the specified geometries to each other. When contact between the two sets of geometry occurs, a force based on the defined physical properties is generated. This represents the contact force. Both normal and frictional forces are modeled. When the bodies separate, the force becomes zero.
There are four key features to the contact capability:
| • | Modeling the geometry of the bodies that are in contact |
| • | Detecting the onset of contact |
| • | Applying the contact force |
| • | Detecting the end of a contact "incident" and removing the contact force |
Two contact types are available: Rigid body to rigid body (MBCNTR) which is defined as the contact of two element sets (SET) and rigid to flexible body (MBCNTDS) which is defined as the contact between a node set (SET) and a deformable surface. The deformable surface must be defined by the MBDSRF bulk data entry.
When the onset of a collision is detected, the collision detection algorithm returns a set of interfering polygons. From those the solver computes the following:
| • | The point of contact and surface normal vector |
| • | The magnitude and direction of the normal and friction forces |
Once the point of contact and surface normal vector are known, the normal and friction force magnitudes are computed using a penalty-based Poisson contact normal force model. The two primary inputs to this model are the penalty and the coefficient of restitution (COR). COR is defined as the ratio of relative speed of separation to the relative speed of approach of the colliding bodies. A COR of 1.0 implies a perfectly elastic collision and a COR of 0.0 represents a perfectly plastic collision. One may think of the COR as damping and penalty as stiffness. Too high of a penalty value may cause numerical difficulties, while too small of a value may lead to excessive penetration. Some fine-tuning of these two parameters is usually required to reach stable and accurate results.
The frictional force is modeled as a viscous force according to the following law:
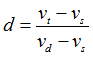
![]()
Where,
![]() is the current slip speed at the point of contact
is the current slip speed at the point of contact
![]() is the coefficient of static friction
is the coefficient of static friction
![]() is the coefficient of dynamic friction
is the coefficient of dynamic friction
![]() is the friction transition slip speed at which the full value of
is the friction transition slip speed at which the full value of ![]() is used for the coefficient of friction
is used for the coefficient of friction
![]() is the dynamic friction slip speed at which the full value of
is the dynamic friction slip speed at which the full value of ![]() is used for the coefficient of friction
is used for the coefficient of friction
![]() is the friction force that is to be applied. The friction force opposes the direction of the slip velocity
is the friction force that is to be applied. The friction force opposes the direction of the slip velocity
See Also: