A multi-body system is defined to be an assembly of sub-systems (bodies, components, or sub-structures). The motion of the sub-systems may be kinematically constrained and each sub-system or component may undergo large translational and rotational displacements.

Bodies can be considered rigid or flexible. Rigid bodies do not undergo deformations. Rigid body motion can be described completely by using six generalized coordinates. The resulting mathematical model is highly nonlinear. Neglecting the body deformations can lead to inaccurate results. Therefore, some of the bodies are considered flexible, that is they can undergo deformations. Modal reduction procedures are used to include flexible bodies in multi-body dynamics simulations.

Joints, force elements, and controls connect the bodies. Initial velocities, forces, and motions may be applied to the system.

Different types of analysis can be performed on a multi-body system to determine its behavior under certain loading, applied motion, and initial velocity. Transient (kinematic, dynamic) analysis determines the response under time dependent loading. Static and quasi-static analyses determine the static equilibrium of a system. The multi-body solution is based on an extended absolute coordinates formulation.

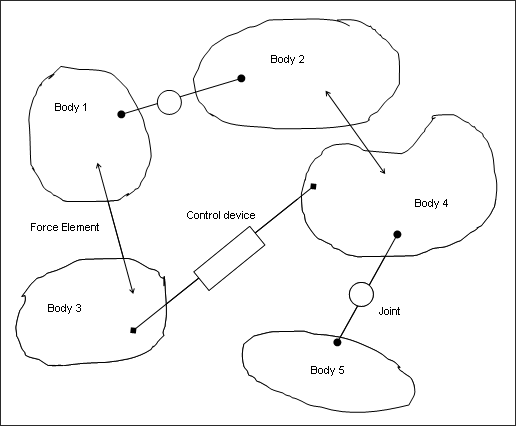
Multi-body system

This implementation is targeted at the typical finite-element user who wants to solve multi-body dynamics problems in the context of a finite element model, and is still somewhat limited. HyperMesh is used for modeling. All geometry entities are defined in terms of a finite element mesh. Flexible body modeling is fully integrated.

HyperStudy can be used for optimization. Shape optimization of rigid and flexible bodies is available through the use of HyperMorph.