|
»Click here to display Table of Contents«
|
Curved Cantilever Beam |
|
|
|
|
|
Curved Cantilever Beam |
|
|
|
|
|
»Click here to display Table of Contents«
|
Curved Cantilever Beam |
|
|
|
|
|
Curved Cantilever Beam |
|
|
|
|
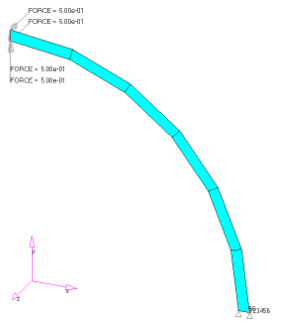
E = 1.0E7; Poisson's ratio = 0.25; Loading; unit force at tip.
This is a curved cantilever beam solved with solid and shell elements. A model is made with each element's type to investigate the effect of distorted elements with a high aspect ratio.
Six types of elements are used for this problem. They are tria-shell, quad-shell, and hexa-solid elements, each with 1st and 2nd order. Two loading cases are used for each model; in-plane bending, transverse bending. For both load cases, unit loads are applied in a consistent fashion over all of the nodes at the tip of the beam.
Theoretical solutions for the deflections at the tip, computed by beam theory, are as follows.
Load Type |
Component |
Value |
in-plane bending |
UY |
0.08734 |
transverse bending |
UZ |
0.5022 |
All results are normalized with the target value.
|
In-plane Bending |
Transverse Bending |
QUAD4 |
0.952 |
0.955 |
QUAD8 |
1.015 |
0.984 |
|
||
TRI3 |
0.025 |
0.950 |
TRI6 |
1.005 |
0.961 |
|
||
HEX8 |
0.880 |
0.820 |
HEX20 |
1.009 |
0.946 |
<install_directory>/demos/hwsolvers/optistruct/CBhex.fem
<install_directory>/demos/hwsolvers/optistruct/CBpent1.fem
<install_directory>/demos/hwsolvers/optistruct/CBpen2.fem
<install_directory>/demos/hwsolvers/optistruct/CBquad.fem
<install_directory>/demos/hwsolvers/optistruct/cbquad2.fem
<install_directory>/demos/hwsolvers/optistruct/cbquad4.fem
<install_directory>/demos/hwsolvers/optistruct/CBtri1.fem
<install_directory>/demos/hwsolvers/optistruct/CBtri2.fem
MacNeal, R.H., and Harder, R.L., A Proposed Standard Set of Problems to Test Finite Element Accuracy, Finite Elements in Analysis and Design, 1 (1985) 3-20.