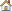For a Michell-truss type solution, a point load is applied at the right hand tip, and nodes along the circle are fixed. The upper half of the system is modeled because of the symmetry (Dimension of the FE model  = 100*30).

CHECKER,2.

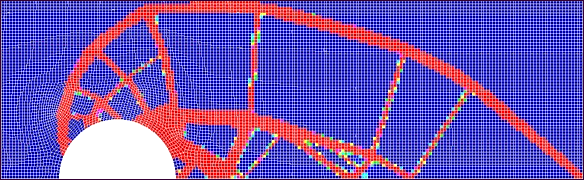
MINMEMB,6.0,1.

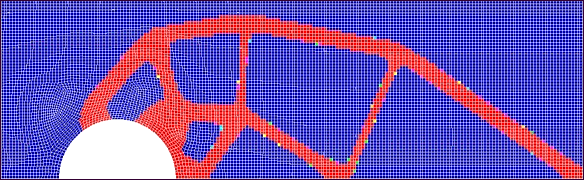
MINMEMB,6.0,2.

In this example, an MBB-Beam with a point load in the upper middle point and two roller point supports at the two lower corners is used. The right half of the beam is modeled (dimension of design domain = 900*300).

DOPTPRM CHECKER 2

DOPTPRM MINDIM  60.0    MINMETH 1

DOPTPRM MINDIM  90.0    MINMETH 1

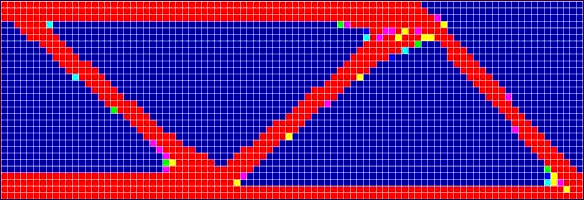
DOPTPRM MINDIM  60.0    MINMETH 2

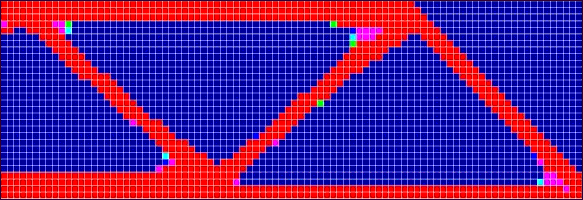
DOPTPRM MINDIM  90.0    MINMETH 2

In this example, an arch with three single point loads as three individual load cases on the lower edge is used. Two roller supports are placed at the two lower corners. The dimension of the domain equals 500*250.

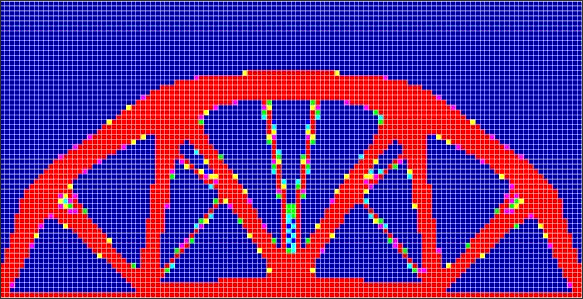
CHECKER, 2.

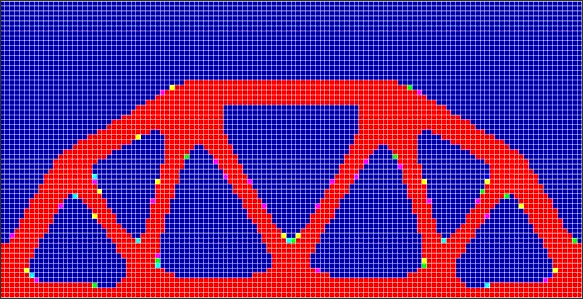
MINMEMB,40.0,1.

In this example, a 3D bridge model with a fixed support at both ends is used. Three load cases: a uniform load p=1 on the entire surface of the bridge and a uniform load p=0.3 on the lanes in each direction separately. The dimension of the design domain: length/width/depth = 500/100/100. Target volume fraction = 0.2.

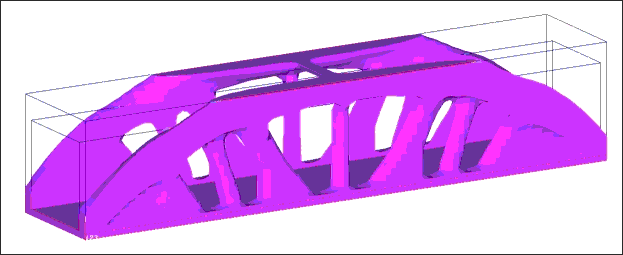
CHECKER, 1.

MINMEMB, 20.0,1.

The reason for running CHECKER=1 in two stages with DISCRETE=1, and then 2, is that after the convergence with DISCRETE = 1, the solution is far from DISCRETE. The two-stage solution provides a fair comparison to results with minimum member control since the latter contains an automatic increase of the DISCRETE value by an increment of 1.