The Johnson-Cook failure model is often used to describe the ductile failure. Stress triaxiality has great influence in ductile material failure. To describe the stress triaxiality in the Johnson-Cook failure model, /FAIL/JOHNSON and /FAIL/SPALLING are most commonly used.

Also, in RADIOSS, BAO-XUE-Wierzbicki failure model (/FAIL/WIERZBICKI) can describe this material character.

In /FAIL/TAB1 tabulated functions can be used to describe the stress triaxiality. /FAIL/TAB1 is based on damage accumulation. Beside stress triaxiality, Lode angle is another important character to describe the material failure, and can also be defined in /FAIL/TAB1 with tabulated function.

Stress triaxiality (normalized mean stress)

Stress triaxiality is an important and useful character to describe the state of stress, which effects the material damage and fracture, as described below:

With Mean stress (hydrostatic stress)

and von Mises stress .

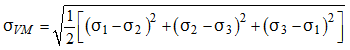
Stress triaxiality special characters are shown below:

In pure tensile:

or, in biaxial compression:

In the Johnson-Cook failure model, there are three parts of material tests:

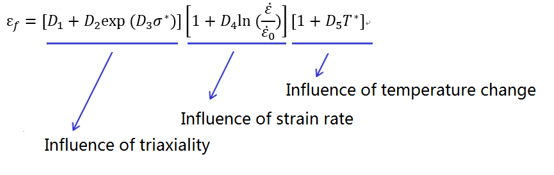
In a simple case, only the first part, triaxiality influence is considered. Then failure strain is:

Parameters D1, D2 and D3 are material constant, and can be found with three of the above specific material tests.

Resulting in three failure strains from uniaxial tension (), pure shear () and uniaxial compression (). Then either D1, D2 and D3 with analytically, or just use Excel to fitting three points with in the curve.

curve describes the material fracture. The material has no fracture, if stress state is under this curve. Once stress state is above this curve, a fracture appears in the material.

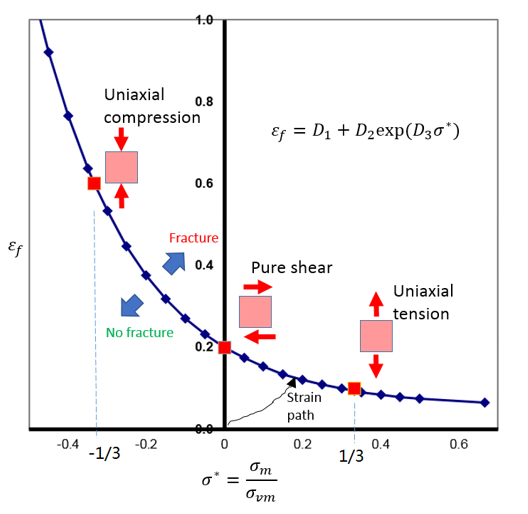
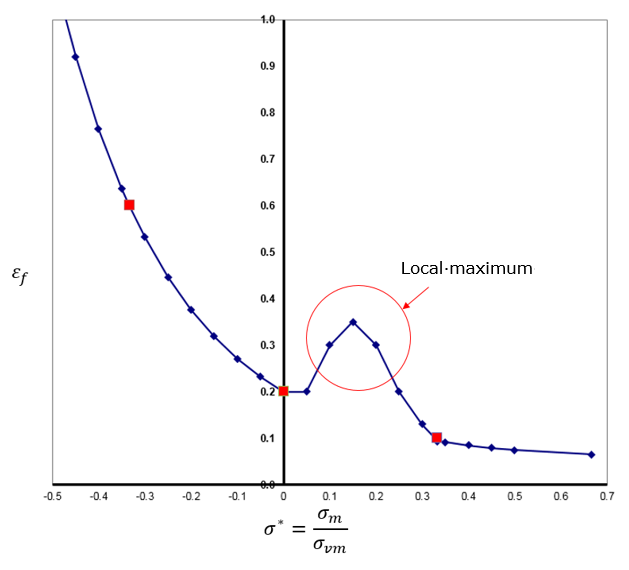
In some cases Johnson-Cook may not be enough with just D1, D2 and D3. These parameters catch the local maximum in curve.

With /FAIL/TAB1, it is possible to input the tabulated function of inside failure strain table.

Lode Angle

In /FAIL/JOHNSON, D1, D2 and D3 describe the failure of shell element, but for solid element, Johnson-Cook failure is not enough. It only describes cases of plane strain, where Lode Angle parameter describes the ductile fracture in a solid.

For Lode Angle parameter you first need to understand what Lode Angle is. The stress state in P could be expressed with principle stress (), but you can also express the stress state in P with hydrostatic stress (pressure, first stress invariant) and deviatoric stress (with second and third stress invariants). The advantage of this expression is that stress invariants are constant and are not dependent on the orientation of the coordinate system, and the invariant of deviatoric stress is frequently used in material failure.

The magnitude of OO’ is

with I1 being the first stress invariant .

OO’ is in the hydrostatic axis, which means the principle stress in this axis is the same (). The magnitude of O’P is .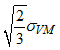

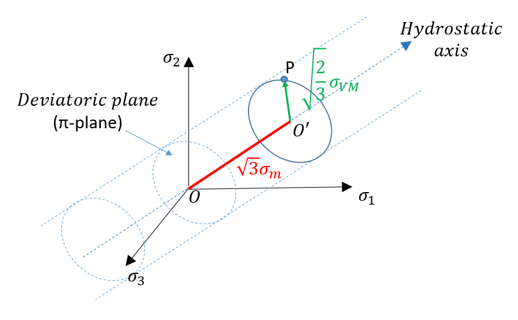
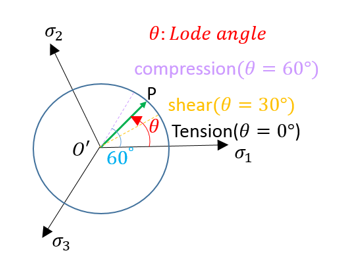
Looking at the projection plane of the deviaotric principal stress, is the Lode Angle, which is:

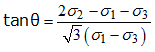
With a range of

The special characters for Lode Angle are:

Use normalized and dimensionless Lode Angle parameter with the range to describe the stress state:

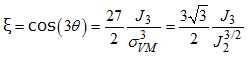
Where, J2 and J3 are the second and third stress invariant.

The special characters for Lode Angle parameter are:

Together with stress triaxiality and Lode angle parameter, the fracture surface of material can be described, as shown below.

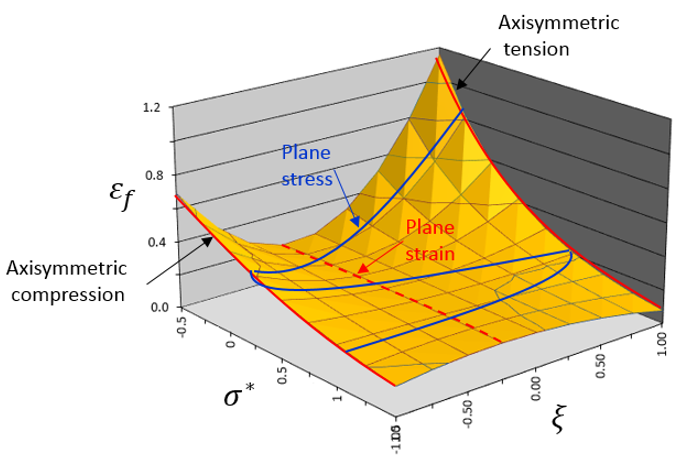
Different material tests will provide results with this fracture surface. Generally, material validation requires more testing to reproduce failure in different loading conditions. In /FAIL/TAB1, use table1_ID to tabulated input function.

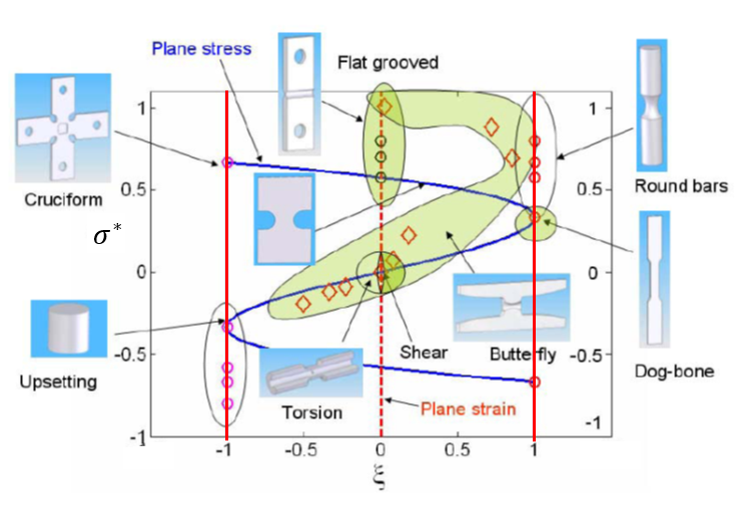
Ranges of stress state attainable by various types of tests [1]

Reference

[1] Wierzbicki, Tomasz, "Addendum to the Research Proposal on "Fracture of Advanced High Strength Steels.", page 19, January 2007.