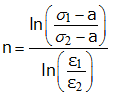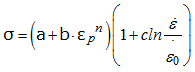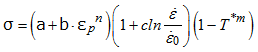In LAW2 there are three parts to the stress calculation.
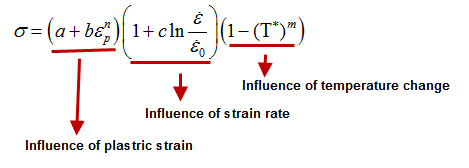
| • | Influence of plastic strain |
| • | Influence of strain rate |
| • | Influence of temperature change |
Influence of plastic strain
There are two ways to input material parameter for LAW2.
| • | Iflag=0: Classic input for Johnson-Cook parameter a, b, n is active |
| • | Iflag=1: New, simplified input with yield stress, UTS (engineering stress), or strain at UTS |
Iflag = 0
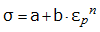
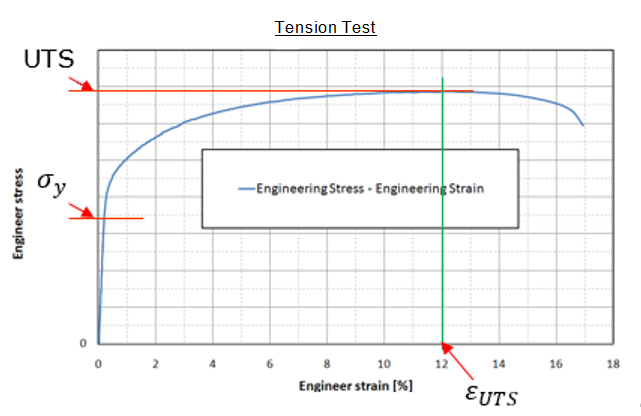
Where, a is the yield stress which could be read from material test and converted to true stress. If you do not have test curve, using Rpo.2 will also convert to true stress.
b and n are the material parameters. Fitting the material stress-strain curve can result in these two parameter. If you do not have stress-strain curve from test, then two stress-strain points are needed to calculate b and n, using the equations shown below. The first point is chosen at the necking point (try to get Rm first), then b and n are computed for each other point of the curve and averaged out since the results tend to differ, depending on the point chosen.
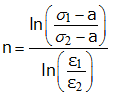
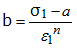
The purpose of this test is to propose a method for deducing material law parameters using a tensile test.
Iflag = 1
With this new input, you will need yield stress (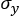 ), Ultimate tensile engineer stress (UTS) and engineer strain ( ), Ultimate tensile engineer stress (UTS) and engineer strain (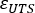 ) at necking point. With this new input, RADIOSS automatically calculates the equivalent value for a, b and n. ) at necking point. With this new input, RADIOSS automatically calculates the equivalent value for a, b and n.

Influence of strain rate
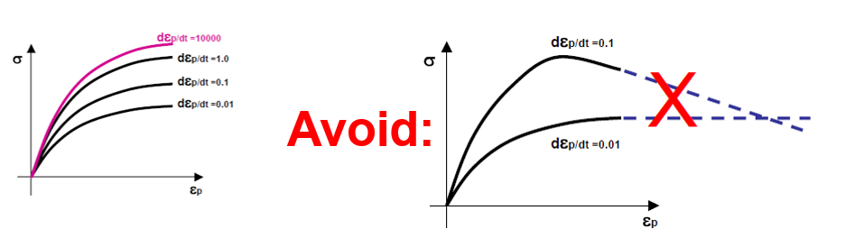
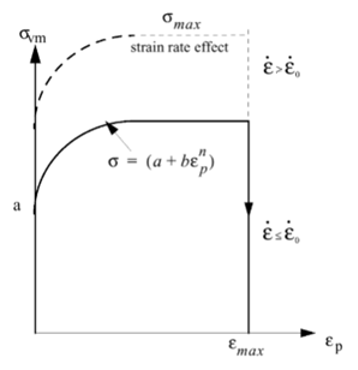
Strain rate has a major effect of material character on crash performance in tensile or in fracture. The yield stress is affected directly by the strain rate, described below:
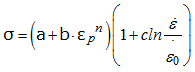
Generally, yield stress increases with increasing the test strain rate. With the strain rate coefficient, c, you can scale the factor of yield stress increase. No effect of strain rate is defined, if c=0; or with 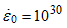 or or 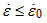 . .
Influence of temperature change
Yield stress decreases with increasing temperature. In LAW2 influence is considered with (1 - T*m).
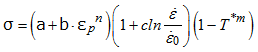
with
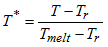
Hardening coefficient Chard
Metal deformed up to yield and then generally hardened (yield stress increased). Different materials show different ways of hardening (isotropic hardening, kinematic hardening, etc.). This is also a very important material character (for spring-back).
In LAW02, use option “Chard” (hardening coefficient) to describe which hardening model is used for the material. This feature is also available in material laws 36, 43, 44, 57, 60, 66, 73 and 74.
The value of Chard is from 1 to 0. Chard =0 for isotropic model, Chard=1 for kinematic Prager-Ziegler model, or between 1 and 0 for hardening between the above two models.
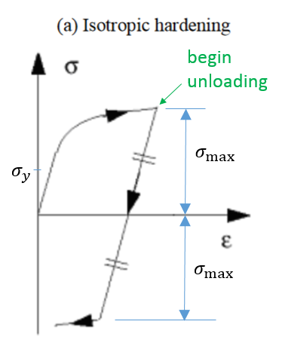
Chard=0: isotropic model
In a one dimension case, material strengthens after yield stress. The maximum stress of the last tension is the yield in the subsequent loading, and this new yield stress is the same in subsequent tension and compression.
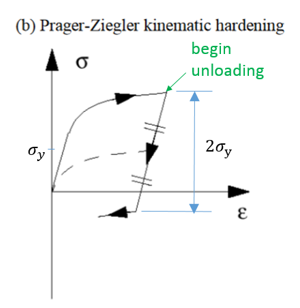
Chard=1: kinematic Prager-Ziegler model
To model the Bauschinger effect (after hardening in tension, there is softening in a subsequent compression which mean yield in compression is decreased), use kinematic hardening.
|