HyperWorks Solvers

Ityp = 1

Ityp = 1

 Previous topic Next topic Expand/collapse all hidden text  

Ityp = 1

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

Block Format Keyword

/MAT/LAW11 - ITYP=1: Boundary Conditions Material in Flow Analysis.

Description

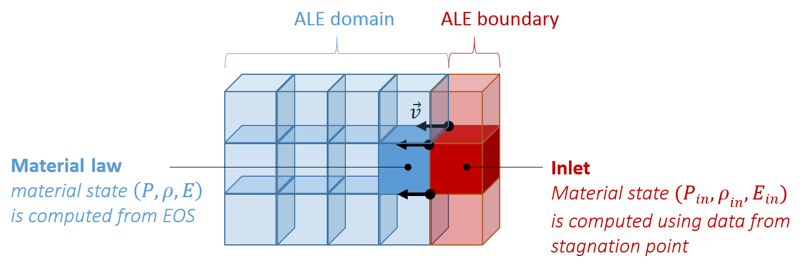
This law enables to model a liquid inlet condition by providing data from stagnation point. Liquid behavior is modeled with linear EOS.

law11_ityp0

Format

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

/MAT/LAW11/mat_ID or /MAT/BOUND/mat_ID

mat_title

 

 

 

 

 

 

Ityp

 

Psh

FscaleT

 

 

 

 

 

Ityp = 1 - Liquid Inlet (from stagnation point data)

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

node_IDV

 

C1

 

 

Cd

 

 

 

 

 

 

 

 

 

 

 

fct_IDp

 

 

 

 

 

 

 

fct_IDE

 

 

 

 

 

 

 

Blank Format

Blank Format

fct_IDT

fct_IDQ

 

 

 

 

 

 

 

 
hmtoggle_plus1Flag Definition

Field

Contents

SI Unit Example

mat_ID

Material identifier

(Integer, maximum 10 digits)

 

mat_title

Material title

(Character, maximum 100 characters)

 

Initial stagnation density (Comment 3)

(Real)

Reference density used in E.O.S (equation of state)

Default (Real)

Ityp

Boundary condition type (Comment 1)

(Integer)

= 0: gas inlet (from stagnation point data)

= 1: liquid inlet (from stagnation point data)

= 2: general inlet/outlet

= 3: non-reflecting boundary

 

Psh

Pressure shift (Comment 2)

(Real)

symbol_Pa

FscaleT

(Optional) Time scale factor (Comment 3)

(Real)

symbol_S_unit

node_IDV

(Optional) Node identifier for velocity computation (Comment 4)

= 0:

> 0:

(Integer)

 

C1

Liquid bulk modulus (Comment 9)

(Real)

 

Cd

Discharge coefficient (Comment 5)

Default = 0.0 (Real)

 

fct_IDdensity

(Optional) Function identifier for stagnation density (Comment 3)

(Integer)

= 0:

> 0:

 

fct_IDp

(Optional) Function identifier for stagnation pressure (Comment 3)

(Integer)

= 0:

> 0:

 

Initial stagnation pressure (Comment 3)

(Real)

symbol_Pa

fct_IDE

(Optional) Function identifier for stagnation density (Comment 3)

(Integer)

= 0:

> 0:

 

Initial specific volume energy at stagnation point (Comments 3 and 8)

(Real)

symbol_Pa

fct_IDT

(Optional) Function identifier for inlet temperature (Comments 3 and 6)

(Integer)

= 0:

= n:

 

fct_IDQ

(Optional) Function identifier for inlet heat flux (Comments 3 and 6)

(Integer)

= 0: no imposed flux

= n:

 
hmtoggle_plus1Comments
1.Provided gas state from stagnation point is used to compute inlet gas state. Bernoulli is then applied.

This leads to inlet state:

   

2.The PSH parameter enables shifting the output pressure, which also becomes P-PSH. If using PSH=P(t=0), the output pressure will be symbol_dp, with an initial value of 0.0.
3.If no function is defined, then related quantity remains constant and set to its initial value. However, all input quantities can be defined as time dependent function using provided function identifiers. Abscissa functions can also be scaled using FscaleT parameter which leads to use f (Fscalet * t) instead of f(t).
4.Inlet velocity ratioin is used in Bernoulli theory.
5.Discharge coefficient accounts for entry loss and depends on shape orifice.

mat_bound_sharpedge

6.With thermal modeling, all thermal data (, …) can be defined with /HEAT.
7.It is not possible to use this boundary material law with multi-material ALE laws 37 (BIMAT) and 51 (MULTIMAT).
8.Definition of stagnation energy is optional. Default value recommended: ; since linear EOS symbol_dp = C1symbol_u does not depends on energy pressure is not affected and the initial energy is also set by you.

Specific volume energy E is defined as E = Eint / V, where Eint is the internal energy. It can be output using /TH/BRIC.

Specific mass energy e is defined as e = Eint / m. This leads to . Specific mass energy e can be output using /ANIM/ELEM/ENER. This may be a relative energy depending on user modeling.

9.Liquid bulk modulus is usually set to , where co is sound speed.