Iform = 4

Block Format Keyword

/MAT/LAW51 - Iform=4: Inlet Boundaries for Multi-Material ALE Law

Description

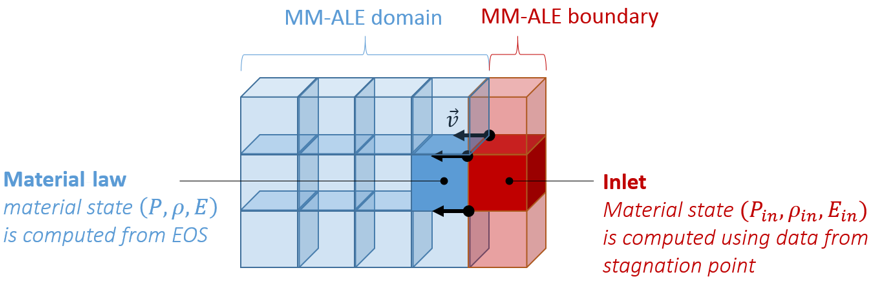
This boundary enables to handle gas inlet conditions for multi-material ALE laws (formulation: Iform = 0, 1, 10, or 11). Boundary sub-material states are computed using provided state at a stagnation point and polynomial EOS. This avoids defining an imposed velocity (/IMPVEL).

Bernoulli theory is applied: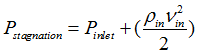

Gas is supposed to be a perfect gas.

law51_iform4

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/MAT/LAW51/mat_ID
mat_title
Blank Format
Iform

#Global Parameters

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Scaletime		PEXT

#Material1 Parameters

(1)	(3)	(5)	(7)	(8)	(9)
		E0mat_1	fct_ID1	fct_ID1	fct_IDE1
C1mat_1			C4mat_1
	C0mat_1

#Material2 Parameters

(1)	(3)	(5)	(7)	(8)	(9)
		E0mat_2	fct_ID2	fct_ID2	fct_IDE2
C1mat_2			C4mat_2
	C0mat_2

#Material3 Parameters

(1)	(3)	(5)	(7)	(8)	(9)
		E0mat_3	fct_ID3	fct_ID3	fct_IDE3
C1mat_3			C4mat_3
	C0mat_3

Field	Contents	SI Unit Example
mat_ID	Material identifier (Integer, maximum 10 digits)
mat_title	Material title (Character, maximum 100 characters)
Iform	Formulation flag (Integer) = 4: Gas Inlet (computed from data at stagnation point)
Scaletime	Abscissa scale factor for input functions (Comment 2) Default = 1 (Real)
PEXT	External (ambient) pressure (Comment 3) (Real)
	Initial volumetric fraction (Comment 4) (Real)
	Initial density at stagnation point (Comment 1) (Real)
E0mat_i	Initial density energy at stagnation point (Comment 5) (Real)
fct_IDi	(Optional) Volumetric fraction scaling function identifier (Comment 6) = 0: > 0: (Integer)
fct_IDi	(Optional) Volumetric fraction scaling function identifier = 0: > 0: (Integer)
fct_IDEi	(Optional) Volumetric fraction scaling function identifier = 0: > 0: (Integer)
C1mat_i	Coefficient for perfect gas EOS (Comment 5) (Real)
C4mat_i	Perfect gas ( - 1) constant (Comment 5) (Real)
C0mat_i	Coefficient for perfect gas EOS (Comment 5) (Real)

1.	Provided gas state from stagnation point is used to compute inlet gas state. Bernoulli theorem is applied:

This leads to inlet state:

Then global material state is determined by computing a mean value:

Pressure:

Density:

Energy:

2.	Provided optional scale function can be used, such as f (Scaletime * t) is used, instead of f(t).

Parameter PEXT takes into account ambient pressure in case you want to work with relative pressure

. This parameter is required by RADIOSS for correct energy integration at each cycle. Otherwise, numerical EOS solving is generally incorrect. It represents pressure which must be added to EOS calculation to obtain total (physical) pressure. It has no influence on pressure contour in animation files.

Example using linear EOS:

Total pressure: , and also PEXT = 0

Relative Pressure: , and also PEXT = Pamb

4.	Volumetric fractions enable the sharing of elementary volume within the three different materials.

For each material, must be defined between 0 and 1.

Sum of initial volumetric fractions must be equal to 1.

For automatic initial fraction of the volume, refer to /INIVOL.

5.	Perfect gas EOS is . Generally it can be written using this general form , where C4 = ( - 1). This provides more flexibility, depending on whether pressure and energy can be total or relative: