In this tutorial you will perform a brake squeal analysis on a brake assembly. Disc brakes are operated by applying a clamping load using a set of brake pads on the disc. The friction generated between the pads and the disc causes deceleration, and can potentially induce a dynamic instability of the system. This phenomena is known as brake squeal. For this model OptiStruct will predict an unstable mode and the instability is seen to occur at the point of mode coalescence, i.e., a pair of modes occur at the same frequency (mode coupling), and one of them is unstable. The unstable mode can be identified during complex eigenvalue extraction because the real part of the eigenvalue corresponding to an unstable mode is positive.
You can further design brake system which can be stabilized by changing the shape of the brake pads or material properties of the brake components to decouple the modes (which is not shown in this tutorial). The purpose of this tutorial is to conduct brake squeal analysis and identify the unstable modes (if they exist).
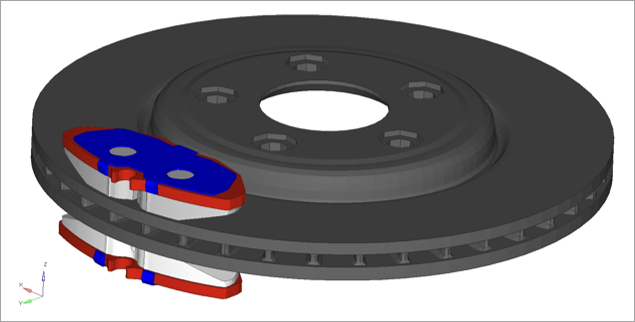
Figure 1. Model review
The following exercises are included:
| • | Set up the problem in HyperMesh |
| • | Submit the OptiStruct job from within HyperMesh |
| • | View the results in HyperView |
Exercise
Setting up the Problem in HyperMesh
Step 1: Launch HyperMesh, set the OptiStruct User Profile and retrieve the structural model
| 1. | Download brsq.fem file from the optistruct.zip file and save to your working directory. Refer to Accessing the Model Files. |
| 3. | Select OptiStruct in the User Profile dialog and click OK. This loads the user profile. It includes the appropriate template, macro menu, and import reader, paring down the functionality of HyperMesh to what is relevant for generating models for OptiStruct. |
| 4. | Click the Import Solver Deck panel toolbar icon  . An Import tab appears. The File type: is OptiStruct. . An Import tab appears. The File type: is OptiStruct. |
| 5. | Click the open file icon  in the File: field. A Select OptiStruct file browser window appears. in the File: field. A Select OptiStruct file browser window appears. |
| 6. | Select brsq.fem from your working directory and click Open. The model file brsq.fem is loaded in the File field. |
| 7. | Click Import to import the file into the current HyperMesh session. |
Information observed in the brsq.fem file
| • | Hexahedral Mesh is created for the brake assembly |
| • | All parts are defined with material MAT1 |
| • | All parts are defined with Solid Element Property |
| • | A cylindrical coordinate system is defined with respect to the disc |
| • | S2S Contacts are defined between brake pad and disc |
Two sub-cases are defined, as shown below:
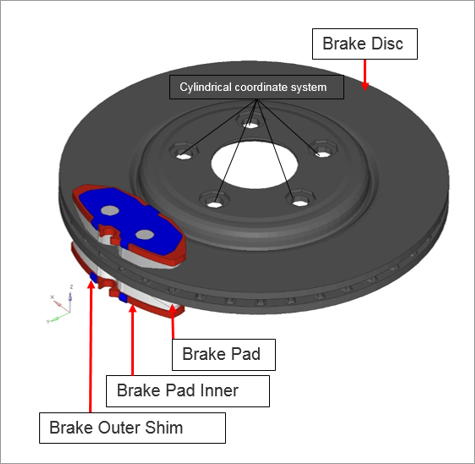
| 1. | Sub-case CLAMPLOAD: Nonlinear static analysis |
Pressure Load on Insulator (Inner and Outer), with SPC (DOF1).
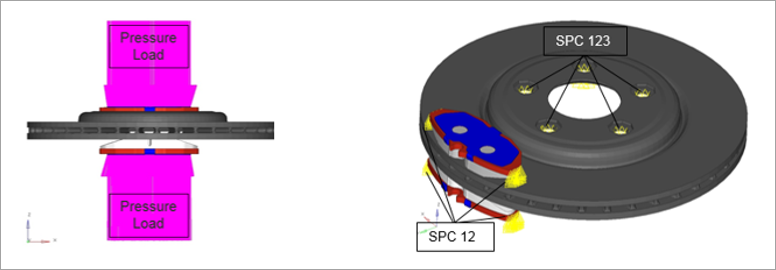
| 2. | Sub-case ROTOR: Nonlinear static analysis with CNTNLSUB |
Pressure Load on Pad and Rotation of the Disc, with non-zero SPC (DOF2).
| Tip #1: | The prescribed rotation should be large enough to ensure the contact between the disc and the pad is in kinetic friction, but small enough to ensure small displacement NLSTAT. |
| Tip #2: | Kinetic friction is a constant value (independent of velocity), hence prescribing rotation using SPCD is equivalent to prescribing rotational speed. The important outcome is that the contact nodes are in kinetic friction mode and it does not matter how fast or how far you move this using SPCD. |
Step 2: Create EIGRL and EIGC cards
In this step, a modal method is used to solve the complex eigenvalue problem, which is more computationally efficient compared to extracting the complex modes directly. With this approach, first, the real modes are calculated via a normal modes analysis. Then, a complex eigenvalue problem is formed on the projected subspace spanned by the real modes which is much smaller than the real space. Here, both EIGRL and EIGC cards need to be defined.
| 1. | In the Model browser, right-click and select Create > Load Collector. |
| 2. | In the Name field, enter modal_space. |
| 3. | Click Color and select a color from the color palette. |
| 4. | Click Card Image and select EIGRL from the drop-down menu. |
| 5. | Click V2 and input 5000. 5000 is defined as the highest frequency bond. |
| 6. | Click ND and input 100. 100 real modes are required to produce the reduced space for complex eigenvalue analysis. |
| 7. | Create another load collector named ceig_squeal. |
| 8. | Click Card Image, and select EIGC. |
| 9. | Click NORM and select MAX. MAX option will be used to normalize the eigenvectors. |
| 10. | Click ND0 and input 55. The desired number of roots to be extracted is 55. |
Step 4: Define a loadstep for modal complex eigenvalue analysis
| 1. | In the Model browser, right-click and select Create > Load Step. |
| 2. | In the Name field, enter BRSQ. |
| 3. | Click Analysis type and select Complex eigen (modal) from the drop-down menu. |
| 4. | For SPC, select DOF2 from the list of load collectors. |
| 5. | For CMETHOD, select ceig_squeal_ from the list of load collectors. |
| 6. | For METHOD(STRUCT), select modal_space from the list of load collectors. |
| 7. | For STATSUB (BRAKE), select Sub-case ROTOR (ID 2). |
| Tip: | Create STATSUB (BRAKE) manually if this is not yet supported in HyperMesh. |
Step 5: Submit the Job
| 1. | From the Analysis page, enter the OptiStruct panel. |
| 2. | Click Save as following the input file: field. A Save As window opens. |
| 3. | Select the directory where you would like to write the file. |
| 4. | In the File name, enter brsq.fem. |
Note the name and location of the file displays in the input file: field.
| 6. | Set the export options: toggle to all. |
| 7. | Set the run options: toggle to Analysis. |
| 8. | Set the memory options: toggle to memory default. |
| 9. | Click OptiStruct. This launches the OptiStruct job. |
If the job completed successfully, new results files can be seen in the directory where the OptiStruct model file was written. Look in the brsq.out file for error messages that will help to debug the input deck, if any errors are present.
Step 6: View the results
Complex eigenvalue analysis computes the complex modes of the structure. The eigenvalues of the complex modes can be found in the brsq.out file. The complex eigenvectors can be reviewed in HyperView.
| 1. | Load the brsq.out file in a text editor. |
The complex modes contain the imaginary part, which represents the cyclic frequency, and the real part which represents the damping of the mode. If the real part is negative, then the mode is said to be stable. If the real part is positive, then the mode is unstable. The eigenvalues of the complex modes are shown below:
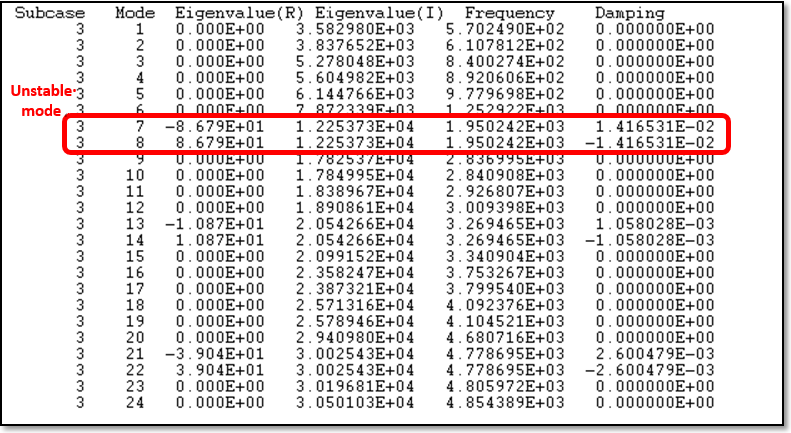
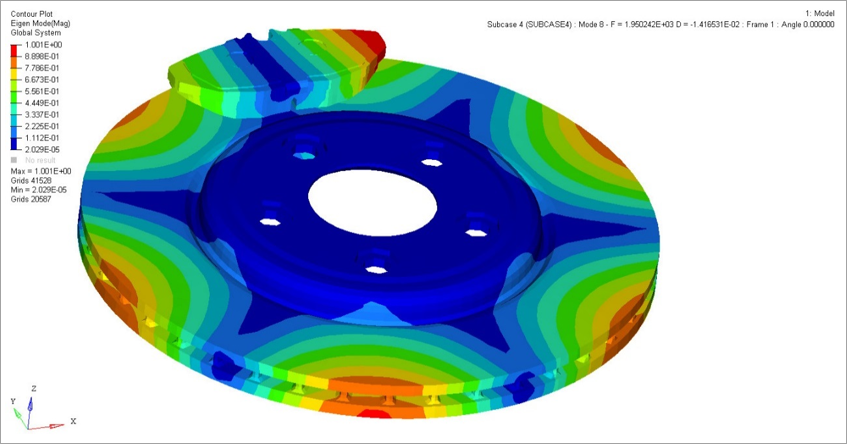
| 2. | Load the brsq.h3d file into HyperView to review complex eigenvectors. |
See Also:
OptiStruct Tutorials













