|
»Click here to display Table of Contents«
|
Prestressed Analysis |
|
|
|
|
|
Prestressed Analysis |
|
|
|
|
|
»Click here to display Table of Contents«
|
Prestressed Analysis |
|
|
|
|
|
Prestressed Analysis |
|
|
|
|
Preloaded or prestressed analysis is any type of structural analysis performed on a structure under prior loading (also termed preloading or prestressing). The response of a structure is affected by its initial state and this is in turn affected by the various preloading/prestressing applied to the structure, prior to the analysis of interest. Examples of prestressed analysis include analysis of rotorcraft blades under centrifugal preloading, pillar-like structures under compressive preloading, preload arising from the pretensioning of bolts on a structure, etc. OptiStruct can be used to take into account such preloading or prestressing effects. The prestressing/preloading loadcase is a linear or nonlinear static loadcase. Prestressed/preloaded analysis is currently supported for linear statics, normal modes, direct frequency response, modal frequency response, direct transient response, and modal transient response analyses. Preloading for a Component Mode Synthesis (CMSMETH) subcase is also supported. Specifying preloading in any other unsupported subcase will generate an appropriate user error. Prestressing is specified through the STATSUB(PRELOAD) Case Control card, which refers to the preloading static loadcase ID. Nested preloading is not supported and will generate an appropriate user error (that is: User error will be reported if Subcase C has preloading from Subcase B, which in turn has preloading from Subcase A).
The preloading is captured or defined by a geometric stiffness matrix KG which is based on the stresses of the preloading static subcase. In prestressed analysis, this geometric stiffness matrix is augmented with the original stiffness matrix K of the (unloaded) structure. Depending on preloading conditions, the resulting effect could be a weakened or stiffened structure. If the preloading is compressive, it typically has a weakening effect on the structure (example: column or pillar under compressive preloading). If the preloading is tensile, it typically has a stiffening effect (for example: rotorcraft blade under centrifugal preloading). For models with contact, the contact status will be carried over from the preloading subcase to the preloaded subcase.
Prestressed static analysis is governed by the following equation, where, f is the load vector and u is the displacement.
While linear static subcases can have prestressing, nonlinear static subcases under prestressing are not supported.
Prestressed eigenvalue analysis is governed by the following equation, where, M is the mass matrix, A is the eigenvector and 
are the eigenvalues.
Prestressed eigenvalue analysis is currently supported by AMSES, AMLS and the Lanczos Method. However, if the specified preload is greater than the first critical buckling load, an appropriate error will be reported for AMSES/AMLS runs.
Prestressed Complex Eigenvalue Analysis is governed by the following equation, where, M is the mass matrix, A is the eigenvector, C is the viscous damping matrix, CGE is the element structural damping matrix, 
is the coefficient of the extra stiffness matrix, 
is the loading frequency, g is the global structural damping coefficient, and Kf is the extra stiffness matrix by direct matrix input.
In addition to Prestressed Complex Eigenvalue Analysis implementation, Brake Squeal Analysis can be performed via the STATSUB(BRAKE) command, wherein the contribution of friction to the stiffness matrix is automatically included. For further information about Brake Squeal Analysis in the User's Guide.
Prestressed direct FRF analysis is governed by the following equation, where, M is the mass matrix, u is the complex displacement vector, CGE is the material damping matrix, C is the viscous damping matrix that includes the Area Matrix for fluid-structure coupling, f is the loading vector, 
is the loading frequency and g is the structural damping
Prestressed modal FRF analysis is governed by the following equation, where, M is the mass matrix, u is the complex displacement vector and d is its corresponding modal value, CGE is the material damping matrix, C is the viscous damping matrix that includes the Area Matrix for fluid-structure coupling, A is the set eigenvectors which includes normal modes and residual vectors, f is the loading vector, 
is the loading frequency, and g is the structural damping coefficient.
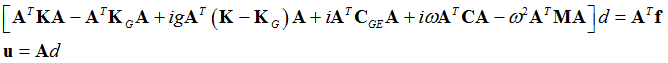
Prestressed direct transient analysis is governed by the following equation, where, M is the mass matrix, u is the displacement vector, C is the viscous damping matrix – which also includes structural damping in an approximate way, and f(t) is the transient load.
Prestressed modal transient analysis is governed by the following equation, where, M is the mass matrix, u is the displacement vector; d is its corresponding modal value, C is the viscous damping matrix – which also includes structural damping in an approximate way, A is the set eigenvectors which includes normal modes and residual vectors, and f(t) is the transient load.
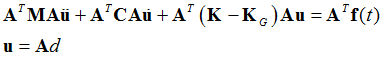
Prestressed Component Mode Synthesis (CMS) uses (K - KG ) as the stiffness matrix, with other aspects such as the mass and damping matrices remaining unchanged in order to calculate the static and normal modes for both flexible body generation (as an input to multi-body dynamics) and direct matrix input generation (for external superelements). The primary effect of a preloaded/prestressed CMS analysis will be a frequency shift in the results.
All results that are supported for regular structural analyses are also available in the corresponding prestressed analyses. It is important to note that, while the prestressed analysis includes the effects of preloading as a weakening or a stiffening of the structure, the results from the prestressed analysis do not include the preloading results. For example, the displacements from prestressed static analysis do not include the preloading displacements. In order to get the overall deflection/stresses of the structure, the displacements/stresses from the prestressed analyses have to be carefully superposed with the preloading displacements/stresses while post-processing. Particularly, while post-processing complex results from prestressed direct FRF, the correct approach would be to first obtain the complex results for a certain phase and then superpose the appropriate preloading result. Any other superposing approach would lead to incorrect results.