Overall, the equation of motion for translational velocities with anti-hourglass and contact forces is written as:

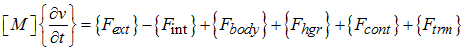
Where, {Ftm} is the transport momentum vector given as:

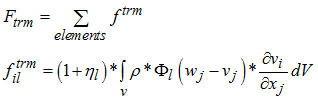
All matrices and vectors defined in the above equation are integrated over the spatial domain. The mass matrix is not constant in time, since the density and domain vary with time. It is shown that the solution of the equation is oscillatory in space when a mesh parameter, known as the Peclet number exceeds a critical value. This spatial stability can be avoided by adding numerical diffusion to the scheme which otherwise is generally under-diffusive and thus unstable. The momentum upwind coefficient is defined in material input. The full upwind case (coef=1) is the default value in RADIOSS and is generally used.

Two upwinding techniques are available in RADIOSS:

SUPG consists in modifying the shape functions to take into account the momentum convection terms. SUPG is activated in the Engine file by:

/UPWM/SUPG

1.

A Taylor development is applied on the velocity vector u, good results are obtained for low mach numbers. The method can be activated in the Engine file by:

/UPWM/TG

fac

Where, fac is a parameter set to inverse of the Mach number (optimal value).