HyperWorks Solvers

Rotating Shell Example

Rotating Shell Example

 Previous topic Next topic No expanding text in this topic  

Rotating Shell Example

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

In some models, the rate of change for the response value with respect to time is very high, and the response is dominant in the design process; this is the case in the following example. The model is a rotating shell structure. A lumped mass is attached to the center of the right hole. The mass of the structure is to be minimized. The driving motion is a rotational velocity at the center of the left hole. Its profile is shown below. The movement of the structure is like the second hand of a watch. Stress of all the elements must be less than an allowable value. Four shape design variables are controllable.

shell_1

Rotating shell

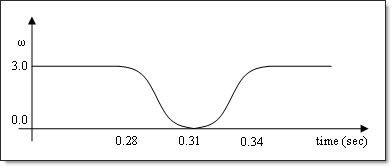
driving_motion_profile

Profile of the driving motion.

After analyzing the initial model, the time history of stress using HyperView can be seen.

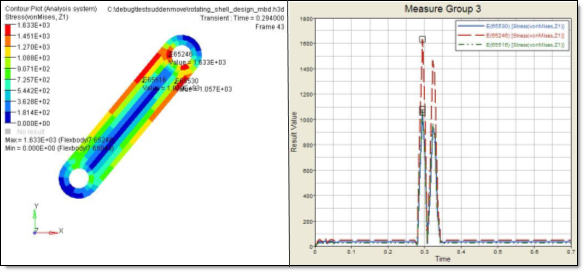
rotating_shell_2

Analysis result of the initial design

According to the analysis result image shown above, the peaks of stress are at around 0.3 seconds. Since the values of these peaks are the largest, you can expect that the responses at around 0.3 seconds will be dominant in the design process. It is a good practice to "zoom in" on the time period around 0.3 seconds so that the optimization process can consider more precise responses. General steps to address the process in this case follow:

1.Run an analysis model with reasonable number of steps in MBSIM card.

ANALYSIS

$

DESOBJ(MIN)=1      

$

SUBCASE       1

 MBSIM =        10

 MOTION =       11

 DESSUB =      11

 SPC = 10

 

       :

       :

 

MBSIM   10      TRANS   END     0.7     NSTEPS   100  

 

Now you can find out the behavior of the structure as in the analysis result image.

2.According to the results post-processed by HyperView, the maximum stresses are developed at around 0.3 seconds. Increase the number of time steps around 0.3 seconds. That is, divide the time period of 0.28 seconds – 0.34 seconds into 200 steps. Increasing the number of time steps in this period provides the optimizer with more information.

The element that has the maximum stress and the corresponding time can be changed as the design changes. Thus, Step 2 does not always work. If the time when maximum stress is developed and corresponding element are expected to change dramatically as the design changes, it is best to consider the changed peak time and corresponding element as much as possible.

3.Replace the previous single MBSIM card with multiple MBSIM cards as the following.

MBSIM   1       TRANS   END     0.28    NSTEPS   50    

+         VSTIFF                

MBSIM   2       TRANS   END     0.34    NSTEPS   200    

+         VSTIFF                      

MBSIM   3       TRANS   END     0.70    NSTEPS   50  

+         VSTIFF    

MBSIM   4       TRANS   END     1.0     NSTEPS   100  

+         VSTIFF            

MBSEQ   10      1       2       3        

 

4.Run the optimization problem by removing ANALYSIS command.

$ANALYSIS

DESOBJ(MIN)=1      

$

SUBCASE       1

 MBSIM =        10

 MOTION =       11

 DESSUB =      11

SPC = 10

 

                  :

                  :

MBSIM   1       TRANS   END     0.28    NSTEPS   50    

+         VSTIFF                

MBSIM   2       TRANS   END     0.34    NSTEPS   200    

+         VSTIFF                      

MBSIM   3       TRANS   END     0.70    NSTEPS   50  

+         VSTIFF    

MBSEQ   10      1       2       3        

 

Using the above steps, the design process convergence can be enhanced.

The input file can be found in <install_directory>/demos/hwsolvers/optistruct/rotating_shell_design.fem.