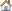Pattern grouping lends itself very well to applications where manufacturing conditions must be met. In the following example, topography optimization is used to form a design concept out of a solid block. Manufacturing the design concept using a casting method is preferable. All optimization set up is done using the optimization panel and its subpanels in HyperMesh.

A solid rectangular block is fixed at both ends and loaded in the center (see Figure 6.1).

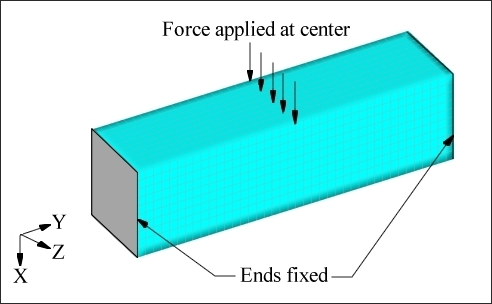
Figure 6.1:  Loads and constraints for the solid block model.

Two shape variables are generated using HyperMesh to control the height and width of the block. These are shown in Figures 6.2 and 6.3.

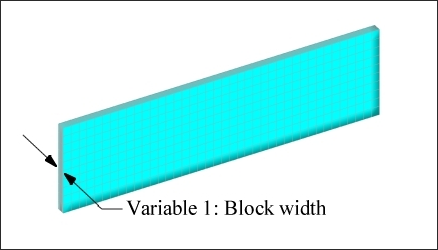
Figure 6.2:  User-defined variable #1.

Figure 6.3:  User-defined variable #2.

It is preferable to manufacture the resulting part using a casting process. This can be accomplished by using a linear pattern grouping in the casting draw direction and a planar pattern grouping perpendicular to the draw. This will ensure that there are no cavities that would create a die lock situation.

Thinking ahead, it is predictable that the cross-section of the solution will be roughly an I-shaped section with the web running vertically. This prediction establishes the draw direction as being horizontal, which corresponds to variable #1 (block width), thus variable #1 will be split using linear pattern grouping and variable #2 will be split using planar pattern grouping. The DTPG cards and associated DESVAR cards are shown below:

The linear variable dispersion pattern for variable #1 allows OptiStruct to control the thickness of the block at numerous points across its side giving the solution a great deal of flexibility. The planar variable dispersion pattern for variable #2 allows OptiStruct to control the height of the cross-sections along the length of the block. The objective was to minimize the mean compliance of the block under the given load. The mass was constrained to be below one fourth of the initial mass of the block. OptiStruct generated the solution, shown in Figure 6.4.

Figure 6.4:  OptiStruct solution for the solid block.

The cross-section of the block is roughly I shaped, concentrating the material at the top and bottom of the end and center areas where the bending moment is the greatest. The design is flat and tall in areas where shear is dominant. The solution is manufacturable by use of a casting process since there are no cavities or die lock conditions. The efficiency of the solution can be seen by looking at the stress contours. The nearly uniform stress distribution, shown in Figure 6.5, indicates that almost every part of the structure is being used to its fullest potential.

Figure 6.5:  Stress contours for the OptiStruct solution.

The maximum dimensions of the block were reduced by 2.5 times and a second topography optimization was performed. The solution OptiStruct produced is shown in Figure 6.6.

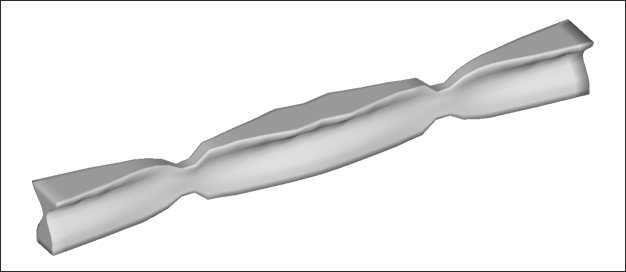
Figure 6.6:  OptiStruct solution for solid block with 2.5 times smaller cross-section.

The basic shape of the block is the same in the reduced dimension model, but has more pronounced features. The I shaped cross-sections in the center and at the ends have wider flanges, and the shear carrying areas in between are thinner. This makes sense considering the smaller dimensions increase the need for bending stiffness more than the need for shear stiffness.

For the input file sample, see <install_directory>/demos/hwsolvers/optistruct/block.fem and <install_directory>/demos/hwsolvers/optistruct/blocklong.fem.

See Also:

Manufacturability for Topography Optimization