Topography optimization has applications beyond creating beads in shell surfaces. Since the basic topography approach can be applied to any model containing large fields of shape variables, it lends itself to solid model applications. The following example demonstrates how topography can be used in conjunction with user-defined shape variables to do global shape optimization of a solid part. All optimization set up is done using the optimization panel and its subpanels in HyperMesh.

A solid control arm model is built based around OptiStruct topology optimization results (see Figure 5.1). Topology optimization is very effective at generating a basic material layout, but the solution is generally not well refined. Refining the solution to meet design specifications can be done using shape optimization. The generation of shape variables over the entire surface of a solid part can be a very time consuming procedure if done by hand. With OptiStruct, this procedure is automated and the shape optimization model can be set up in minutes.

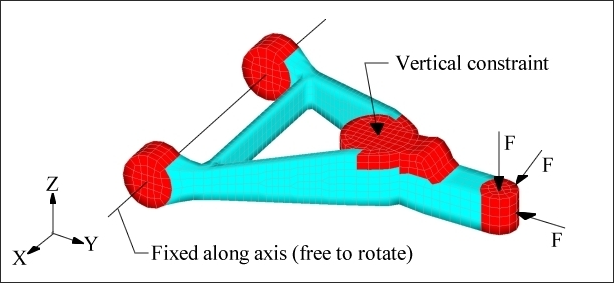
Figure 5.1:  Loads and constraints for solid control arm.

The first step is to generate shape variables for the part. HyperMesh is an excellent tool for doing this. For this model, four basic shape variables were created which control the sizes of the two legs and rear beam of the control arm. These are shown below in Figures 5.2 and 5.3. Care was taken to ensure that the final design would have no internal cavities which would prevent it from being manufacturable.

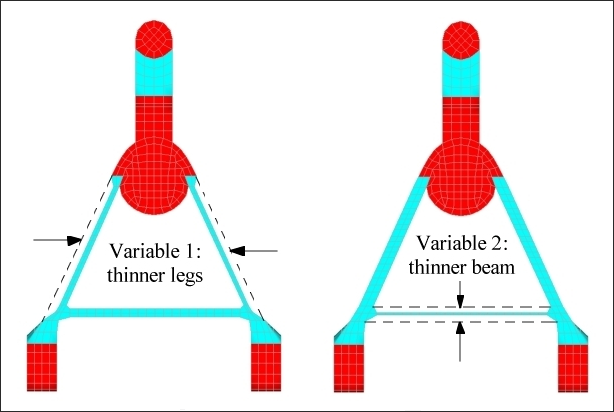
Figure 5.2:  Shape variables controlling the thickness and height of the control arm legs.

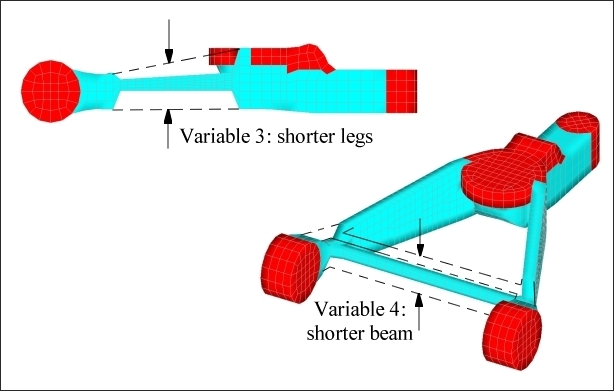
Figure 5.3:  Shape variables controlling the thickness and height of the control arm rear beam.

Topography optimization will divide these shape variables into smaller variables that control the height and thickness of sections of each leg. The type of pattern grouping selected for each variable is used to control the way that the variables get divided. Pattern grouping enhances the ability of topography optimization to affect the shape of solid models. Without pattern grouping, the distance that a grid is allowed to move must be less than the distance to the neighboring grid or else the elements will get turned inside out. With pattern grouping, the movement of several grids can be linked together so that those grids can move far beyond their original positions while still maintaining a reasonable element mesh (as demonstrated in this example problem).

Linear pattern grouping is applied to the first variable which links the movement of all of the grids through the thickness of both legs together. This allows the thickness of the legs to change at many points across the sides of the legs, which gives OptiStruct a high degree of flexibility in influencing their shape without causing problems with the finite element mesh.

Planar pattern grouping is applied to the second variable which links the movement of all of the grids through both the thickness and height of both legs together. This allows the height of entire cross-sections of the legs of the control arm to change. One of these planes is shown in Figure 5.4 cutting through both legs of the control arm.

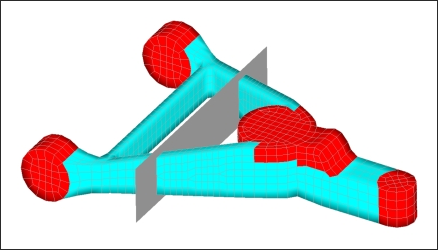
Figure 5.4:  Pattern grouping plane for variable #2.

Figure 5.5 shows the variables created from the planar pattern grouping option. Note that Figure 5.5 only shows the deflections of the centers of the variables. Because of the way that topography optimization works, if all three variables were fully deflected, the legs of the control arm would be uniformly at the minimum height.

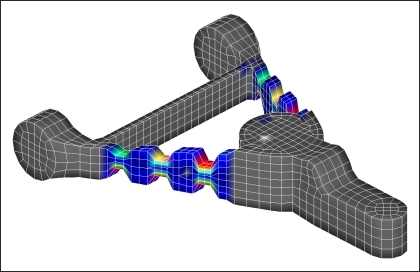
Figure 5.5:  Planar variable dispersion pattern for the height of the legs of the control arm.

Planar variable pattern grouping was also used for the height and thickness of the rear beam. For both variables cards, TYP = 13 was used to ensure a beam shape that was symmetric about the center. The DTPG card for variable #4 (beam height) and the associated DESVAR card are shown below.

Since shape variables are being assigned to topography, the height and the bounds in the DTPG card do not need to be defined, as they are controlled by the shape variable. Even if these values are defined, OptiStruct will ignore them.

The objective for the optimization was to minimize the mean compliance of the control arm for all three load cases combined. The mass of the control arm was constrained to be less than 10% below its initial mass. OptiStruct generated the following solution (see Figure 5.6). The red shows areas where material was added, the blue shows areas where material was removed.

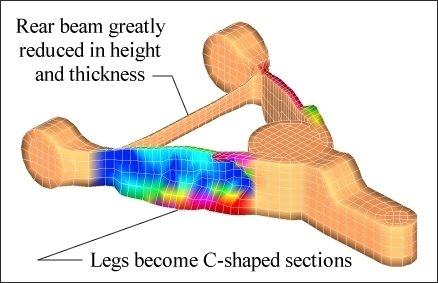
Figure 5.6:  Optimized control arm using topography and user-defined shape variables.

OptiStruct optimizes the shape of the legs by shifting mass from the centers to the top and bottom, creating C-shaped sections. These sections add vertical bending stiffness while leaving the shear and axial stiffness intact. Additionally, the height of the legs was increased along their length to further increase the bending stiffness of the sections. OptiStruct greatly reduced the size of the rear beam in both height and thickness, indicating that it was oversized or perhaps even unnecessary. Overall, the maximum deflection for all three load cases was reduced by 5% while the mass was reduced by 10%. Figure 5.7 shows a refined finite element model of the OptiStruct solution.

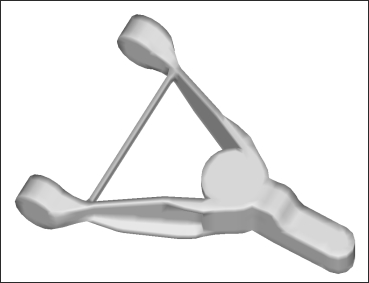
Figure 5.7:  Finite element model of the OptiStruct solution.

For the input file sample, see <install_directory>/demos/hwsolvers/optistruct/controlarm.fem.

See Also:

Manufacturability for Topography Optimization