Pattern grouping and shape variables can be used to optimize stamped plates that are difficult to deal with due to corners and sharp edges. Automatic generation of topography variables does not take into account situations in which elements can be folded inside out when the variables are fully perturbed. This limits the draw depth that can be used with that technique. The following example demonstrates how this problem can be avoided with user-defined variables. All optimization set up is done using the optimization panel and its subpanels in HyperMesh.

A hat section is centrally loaded, creating both bending and torsional loads (see Figure 4.1). The hat section is constrained at either end by four bolts.

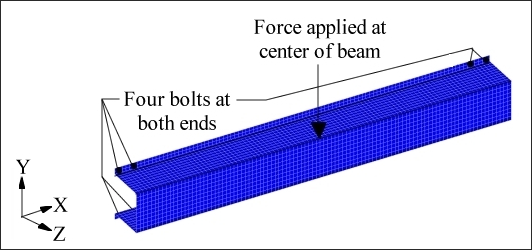
Figure 4.1:  Loads and constraints for the stamped hat section.

It is preferable to have the size of the reinforcements able to run deeper than the height of a single element. To ensure that this will not cause a problem with the element mesh, three shape variables are created using HyperMesh and are added to the deck. The shape variables for the face and top side of the hat are shown in Figure 4.2.

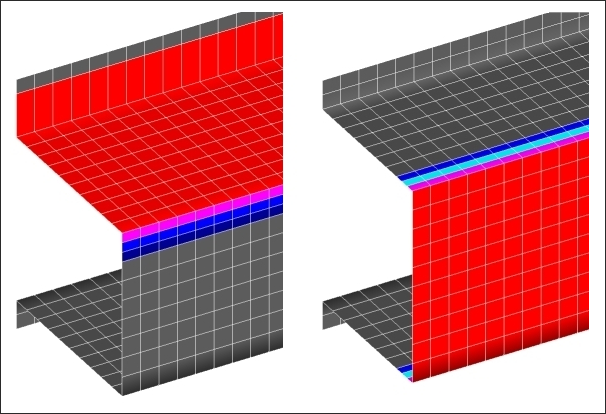
Figure 4.2:  User-defined shape variables for the hat section.

Note in Figure 4.2 that the first three rows of elements adjacent to the elements being fully deflected are a part of the user-defined shape variable for that side. Also, the draw depth is equal to one and a half times the average element size.

It is desired to create this hat section using a stamping process which means that reinforcing features on the sides of the hat must be constant (from top to bottom), or else a die lock condition will occur. Pattern grouping can be used to create variables that ensure manufacturability. For the three variables created for the hat section optimization, planar pattern grouping was selected with the planes running perpendicular to the length of the section (X-axis). The DTPG card and associated DESVAR card for one of the variables are shown below.

Additionally, a plane of symmetry was used to force both halves of the section to be the same.

Figure 4.3 shows the symmetry plane for the hat section.

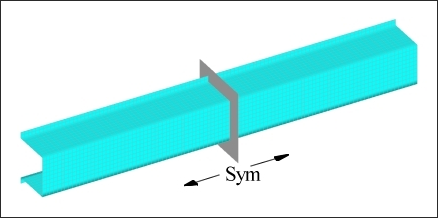
Figure 4.3:  Plane of symmetry for the hat section model.

OptiStruct generates variables which allow for great flexibility in the reinforcement possibilities, but which prevent a die lock condition as shown in Figure 4.4. Note that the area where the load is applied is left out of the face variable.

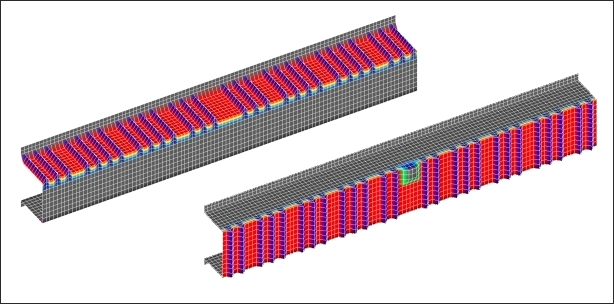
Figure 4.4:  Variables generated for the hat section.

The objective is to minimize the compliance for the applied load. OptiStruct generated the shape shown in Figure 4.5.

Figure 4.5:  OptiStruct solution for the hat section optimization.

The solution generated by OptiStruct is manufacturable using a stamping process. Also, the solution is very well behaved and needs little refinement to turn it into a production-ready design.

The optimized hat section increases the stiffness of the part by more than eightfold from the initial condition with no beads. The eight ‘square’ beads for the hat section, especially the four at the ends of the beam, are the key to bolstering the beam against shear collapse. Those beads also serve to prevent the flanges from folding under the bending load. OptiStruct has generated a strong design that supports both torsion and bending with restricted reinforcement possibilities. The shape and placement of the reinforcements are optimized resulting in a very efficient solution.

For the input file sample, see <install_directory>/demos/hwsolvers/optistruct/hat.fem.

See Also:

Manufacturability for Topography Optimization