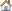A rectangular thin-walled box is to be used to store fluid. The outward bulging of the sides of the container (due to the pressure of the contents) is to be minimized. Additionally, the maximum outward displacement of the side panels must be below a given value. The model is shown in Figure 3.1. All optimization set up is done using the optimization panel and its subpanels in HyperMesh.

The model is constrained for displacement in all directions at the four lower corners but is free to rotate about those constraints. The loading is a distributed pressure through the area shown in green. The pressure is higher at the bottom of the vessel.

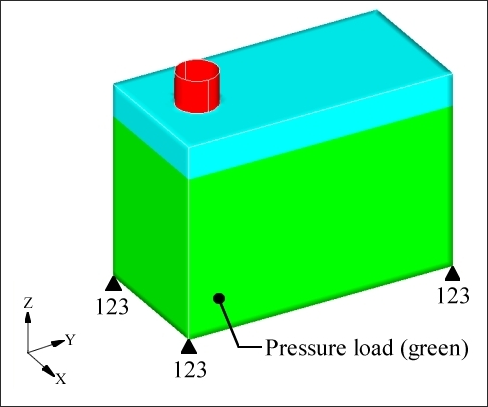
Figure 3.1:  Loads and constraints on rectangular pressure vessel.

The entire box is to be used as the design domain with the exception of the filling hole on the top shown in red. All of the elements in the design domain are placed in the same component and reference the same material property. The normal vectors for all of the elements in the design domain are pointing outward. The topology variables are set up with the following DTPG card:

Three orthogonal planes of symmetry are defined (see Figure 3.2). The anchor node is placed at the center of the box. The first and second vectors are defined parallel to the X and Y axes. The first vector is defined pointing away from the filler cap. This ensures that the automatically generated variables will cover the entire surface of the box. If the first vector was pointing in the other direction, the symmetry method would reflect the lack of variables in the area of the filler cap across all three planes of symmetry.

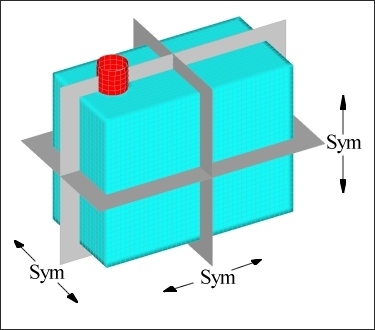
Figure 3.2:  Orthogonal symmetry planes for the pressure box.

The objective is to minimize compliance for the pressure load case, which is the same as minimizing the strain energy of the entire model. The displacement of the center point of each of the five loaded surfaces was constrained to be less than a given value.

OptiStruct generated the following solution for the pressure box shown in Figure 3.3.

Figure 3.3:  OptiStruct solution for the pressure box.

The OptiStruct solution met all of the optimization constraints and yielded a good design. The areas shown in red (In Figure 3.3) are the bead reinforcements that OptiStruct created to increase the stiffness of the model. The solution is unconventional, but makes a good deal of engineering sense. For the large side panels and the top and bottom panels of the box, OptiStruct has generated large, rounded, centrally located reinforcement beads. These types of beads are very effective in stiffening the panels against a distributed or central load. This is due to the fact that bending in the central areas of the panels is occurring in two directions, both vertically and horizontally. The rounded beads create stiffness in both directions and are weak in neither. At the eight corners of the model, OptiStruct created beads that anchor the sides of the box together allowing each side of the box to gain support from the neighboring sides.

A finite element model was created from this reinforcement pattern (see Figure 3.4).

Figure 3.4:  Finite element model of the OptiStruct solution for the pressure box.

This pattern was compared to two other bead reinforcement designs shown in Figure 3.5.

Figure 3.5:  Conventional reinforcement patterns for the pressure box.

The OptiStruct model is superior in stiffness to both of the two conventional models. The maximum deflection of the OptiStruct model was 30% less than the lightly reinforced conventional model (the one on the left), and 46% less than the heavily reinforced model (the one on the right). The lightly reinforced model was stiffer than the heavily reinforced model, which goes against the assumption that more reinforcements result in increased stiffness. With bead type reinforcements that assumption is not always true, which demonstrates the effectiveness of topography optimization. OptiStruct delivers an optimized first design, eliminating the need to do a series of re-designs where the second, third, fourth, etc., model does not always result in an improvement.

Manufacturing constraints can be accounted for in the pressure box model using other pattern grouping options. The set up is done easily through the HyperMesh interface. In order to manufacture the pressure box using a two piece die mold, bead reinforcements that run laterally would need to be eliminated or else they would cause a die lock condition. Topography optimization can be used to generate reinforcement beads on the sides of the box that run vertically only. This is done by using separate topography variables for the side walls, front and back panels, and the top and bottom panels. Topography variables with planar symmetry with one plane symmetry grouping type are defined for the side panels and the front/back panels, respectively. As in the earlier case, a three plane symmetry topography variable is assigned for the top/bottom panels. The two cards are shown below and differ only in the direction of the first vector.

The planes for the planar pattern grouping run vertically and perpendicular to the Y-axis, which causes OptiStruct to generate vertical beads. Because the planes run through both sides of the box, there will be symmetry between opposing sides. Also, symmetry on either side of the anchor node in the direction of the first vector (Y-axis) is forced with the one plane symmetry option (pattern grouping option 13). See Figure 3.6.

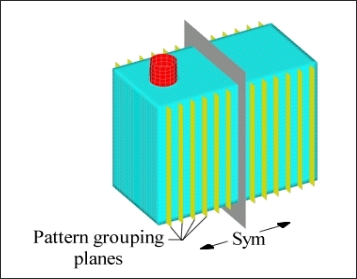
Figure 3.6:  Planar pattern grouping planes for sides of pressure box.

With planar symmetry enforced for the sides of the pressure box and three-plane symmetry enforced on the top and bottom of the box, OptiStruct generated the solution shown in Figure 3.7. Even without the presence of lateral beads on the sides of the box, the OptiStruct solution shown below had a maximum deflection 6% less than the lightly reinforced conventional model.

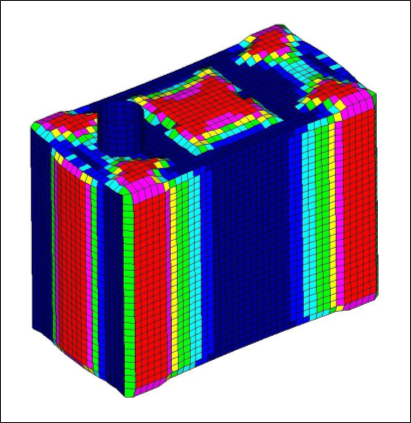
Figure 3.7:  Pressure box solution for combined three-plane and planar symmetry options.

For the input file sample, see <install_directory>/demos/hwsolvers/optistruct/pressure.fem and <install_directory>/demos/hwsolvers/optistruct/pressure13.fem.

See Also:

Manufacturability for Topography Optimization