In this tutorial you will,
| • | Perform an optimization study in the MotionView-HyperStudy environment |
| • | Compare the baseline and optimized models |
Theory
In general, an optimization problem consists of:
Design variables change during optimization. The design variables always have a certain range within which they can be modified. Typical examples of design variables are thickness of shell elements, shape vectors, and masses.
The changes in the design variables cause some change in model responses. Such responses can become either objective function or design constraints. Examples of such responses include displacements and forces.
The response to be minimized or maximized becomes the objective function, while the rest of the responses that need to be within a certain tolerance range become constraints. Only one response can be defined as objective function.
HyperStudy can be used to set-up and perform an optimization study on a MotionView model. You can also use HyperStudy to perform optimization studies involving both linear and non-linear CAE analysis as well as perform optimization of mathematical equations using Templex. HyperStudy creates the input parameter files using Templex and provides iterative changes to them during the optimization process. HyperStudy uses HyperOpt (a general purpose, wrap around software) as the optimization engine to perform optimization, in conjunction with both linear and non-linear CAE analysis software. HyperOpt uses a robust sequential response surface methodology for optimization.
The files needed for this tutorial are hs.mdl, target_toe.csv (used in tutorial MV-3000); Setup.xml saved in tutorial MV-3000 and the nom_run folder created in tutorial MV-3000.
These files should be in the <working-directory> that was used in tutorial MV-3000.
| Note: | If you copy the Setup.xml file from the above location, the path in the <Folder> tag in the file needs to be edited to point to your <Working directory>. |
In the following steps you will perform an optimization study on a front SLA suspension model and determine the optimum coordinate positions of the inner and outer tie-rod points while trying to achieve a target toe curve. The baseline model will then be compared with the optimized model.
Step 1 Optimization Study.
| 1. | Start a new MotionView session. |
| 2. | Open the model hs.mdl, located in <working directory>. |
| 3. | Review the model and the toe-curve output request. |
| 4. | From the SolverMode menu make sure that MotionSolve is selected. |
| 5. | From the Applications menu, launch HyperStudy. |
| 6. | Click on open file icon,  , browse to your study directory and select Setup.xml file created during the MV-3000 tutorial. |
| 7. | Add a new optimization study: |
| - | Right-click in the Explorer Browser area and from the context menu, click Add Approach to launch the HyperStudy - Add dialog box. |
Or
| - | From the Edit menu bar, click the Add Approach icon,  , to launch the HyperStudy - Add dialog box. |
| - | Under Select Type, select Optimization. |
| - | Accept the default label and variable name and click OK. |
| - | The Optimization tree displays in the explorer with name Optimization_1. |
| - | Click Next to go to the Select design variables. |
| 8. | In the Define design variables panel, verify that all the design variables are checked. |
This panel displays all the variables and their upper and lower bounds.
| 9. | Click Next to go to the Select responses. |
| - | Click  to launch the HyperStudy - Add Objective dialog box. |
Accept the default label and variable names and click OK.
In this exercise, minimize the Sum of Squared Error response function to obtain optimum values for the design parameters: the Y and Z coordinate positions of the inner and outer tie-rod points.
| - | Check to make sure that the type is set as Minimize from the drop-down menu. |
| - | Check to make sure that the Evaluate From option is set to Solver. |
| 10. | We will not have any constraints and unused responses in our design, so click Apply and then click Next to go to Specifications. |
Accept the default Optimization Engine: Adaptive Response Surface Method and click Apply and Next. The Maximum iterations and Convergence criteria are specified in the same dialog.
| 11. | Click Apply and Next to go to Evaluate. |
| 12. | Click Evaluate Tasks to start the optimization. |
MotionSolve is launched sequentially and the HyperOpt engine attempts to find a solution to the problem.
Once the optimization is complete, an Iteration table is created with status of each run. The present study took nine iterations to achieve the target. Browse through the other tabs of this page to get more understanding of the iteration history.
| 13. | Click on the Iteration Plot 2D tab. |
| 14. | From the list on the right side of the GUI, select the Objective function named Objective_1 . |
This plots the objective function value against the iterations.
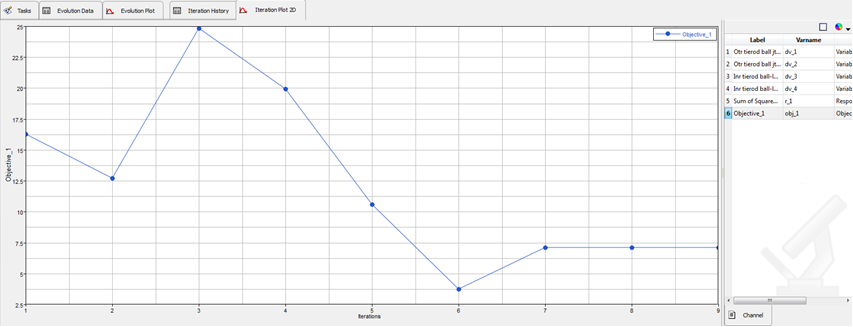
Optimization history plot
In this panel, you can see the plots variations in the values of the objectives, constraints, design variables, and responses during different design iterations. The Iteration History Table displays the same data in a tabular format.
Note that in this study, iteration 6 is the optimal configuration.
Save your study to <working directory> as Study_2.xml.
Step 2: Comparing the Baseline and Optimized Models.
| 1. | Add a Page to your MotionView session. |
| 2. | From the Select application drop-down menu, select HyperView. |
| 3. | Load the animation file <working directory>\approaches\nom_1\run__00001\m_1\m_1.h3d using the Load Model panel. |
| 4. | Click the Page Layout icon on the toolbar and select the two-window layout. |
| 5. | In the second window, switch to HyperGraph. |
| 6. | Click the Build Plots icon on the toolbar. |
| 7. | Use the Build Plots file browser and select the file target_toe.csv, located in the <working directory>. |
| 8. | For X-axis data, select: |
Type = Unknown
Request = Block 1
Component = Column 1
| 9. | For Y-axis data, select: |
Type = Unknown
Request = Block 1
Component = Column 2
| 11. | Using the file browser on the Build Plots panel, select the file <working directory>\approaches\nom_1\run__0001\m_1\m_1.abf |
| 12. | For X-axis data, select: |
Type = Expressions
Request = REQ/70000033 toe-curve
Component = F2
| 13. | For Y-axis data, select: |
Type = Expressions
Request = REQ/70000033 toe-curve
Component = F3
| 15. | Plot another curve from the file |
<working directory>\approaches\opt_1\run__00006\m_1\m_1.abf using steps 11-14
You should end up with a session looking like the one shown below. Notice the optimized toe-curve.
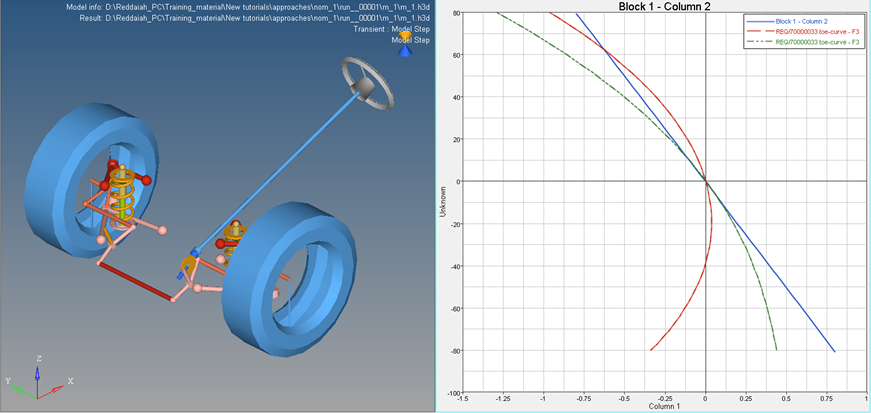
Optimization results
You may also overlay the animation of the optimal configuration (run 6) over the nominal run. Notice the toe angle differences.
Save the session as opt_toe.mvw.
