In exponential biasing, the sizes of the intervals grow geometrically, progressing along the edge, with each successive interval being a constant factor larger than the previous. That factor is 1.0 plus 1/10 of the absolute value of the biasing intensity.  This formula was chosen so that an intensity of zero will still represent no biasing, and convenient values will fall in the range [0,20].  Negative biasing intensities just reverse the edge, placing the smaller elements at the end instead of the beginning.

Specifically, let n be the element density and let .

 

We want a node placement function x(s) taking values in [0,1] with x(0) = 0 and x(1) =1.

 

Let be the geometric growth factor.

 

We need a function so that: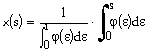

 

Let  then:

which gives the proper interval lengths,

 

then x(s) scales them to the range of [0,1].  Thus, .

See Also:

Element Biasing

Automeshing Secondary panel