In bellcurve biasing, nodes are distributed long the edge in a pattern that is symmetric across the midpoint of the edge. If the biasing intensity is positive, the smaller intervals are placed at the beginning and end of the edge, and if it is negative, they are placed at the middle of the edge.

Specifically, let n be the element density and .

We need so that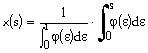

takes values in  [0,1] with x(0) = 0, x(1) = 1, and has the behavior noted above.  If we use:

for positive biasing intensity r, then x(s) becomes:

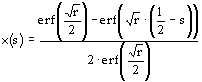    where erf() is the statistical error function,

.

.

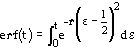See Also:

Element Biasing

Automeshing Secondary panel