HyperStudy

HS-1050: Registering Python Functions in HyperStudy

HS-1050: Registering Python Functions in HyperStudy

 Previous topic Next topic Expand/collapse all hidden text  

HS-1050: Registering Python Functions in HyperStudy

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

In this tutorial you will learn how to register a python function in HyperStudy using the Preference file (.mvw) and then use the registered function for output response evaluation in the study. The Rosenbrock function is defined as a python script and registered in HyperStudy. The example defines two input variables labeled x and y, respectively.  The objective of the optimization is to minimize f(x,y)= 100*(y-x^2)^2 + (1-x)^2.  The range for x and y is set to [-2 ; 2] , and the start point is [1.2 ; 1.1].

The files used in this tutorial can be found in <hst.zip>/HS-1050/. Copy the tutorial files from this directory to your working directory.

hmtoggle_plus1greyStep 1: Create the Python Function
1.In your favorite text editor, enter the following python commands:

def ros_eval(x, y):

   return 100*(y-x*x)*(y-x*x) + (1-x)*(1-x)
2.Form the menu bar, click File > Save As.
3.In the Save As dialog, navigate to your working directory and save the file as rosenbrock_func.py.

 
hmtoggle_plus1greyStep 2: Add the Function to a Preference File
1.In a text editor, enter the following pyton registration function:

*Id("HyperStudy v14.0")

*BeginDefaults()

*BeginPlotDefaults()

*RegisterPythonFunction("ros_eval","<path>/rosenbrock_func.py",2)

*EndPlotDefaults()

*EndDefaults()
2.Replace <path> with the actual location of the .py file.
3.Save the file as a preference file with the name py_prefs.mvw file.
4.Close the text editor.

 
hmtoggle_plus1greyStep 3: Perform the Study Setup
1.Start HyperStudy.
2.From the menu bar, click File > Use Preferences File.
3.In the HyperStudy - Set Preference File dialog, open the py_prefs.mvw file.
4.To start a new study, click File > New from the menu bar, or click files_new_hst2 on the toolbar.
5.In the HyperStudy – Add dialog, enter a study name, select a location for the study, and click OK.
6.Go to the Define Models step.
7.Add an Internal Math model.
a.Click Add Model.
b.In the HyperStudy - Add dialog, select Internal Math and click OK.
8.Go to the Define Input Variables step.
9.Add input variables.
a.Click Add Input Variable.
b.In the HyperStudy - Add dialog, add two input variables labeled X and Y.
c.Change both input variable's lower, initial and upper bounds to the values indicated in the image below.

hs_1500_bound_values

10.Go to the Specifications step.

 
hmtoggle_plus1greyStep 4: Perform the Nominal Run
1.In the work area, set the Mode to Nominal Run.
2.Click Apply.
3.Go to the Evaluate step.
4.Click Evaluate Tasks. An approach/nom_1/ directory is created inside the study directory.
5.Go to the Define Output Responses step.

 
hmtoggle_plus1greyStep 5: Create and Define Output Responses
1.Click Add Output Response.
2.In the HyperStudy - Add dialog, add one output response.
3.In the Expression column of Response 1, click hs_popupdialogicon.
4.In the Expression Builder, click the Functions tab.
5.From the list of available functions, select ros_eval.
6.Click Insert Varname. The function ros_eval() appears in the Evaluate Expression field.
7.Click the Design Variables tab.
8.In the work area, select the input variables X and Y.
9.Click Insert Varname. The input variables appear in the expression as ros_eval(XY).
10.In the Evaluate Expression field, enter a comma in-between the input variables X and Y.

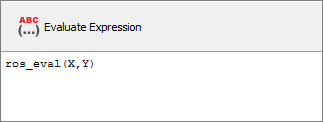
hs_1500_ros_eval

11.Click Evaluate Expression. The expression ros_eval(X,Y) changes to 404.
12.Click OK. This completes the study setup.

 
hmtoggle_plus1greyStep 6: Run an Optimization Study
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Optimization and click OK.
3.Go to the Select Output Responses step.
4.Click Add Objective.
5.In the HyperStudy - Add dialog, add one objective.
6.In the Type column, select Minimize.

hs_1500_objective

7.Click Apply.
8.Go to the Specifications step.
9.In the work area, set the Mode to Adaptive Response Surface Method (ARSM).
Note:Only the methods that are valid for the problem formulation are enabled.
10.Click Apply.
11.Go to the Evaluate step.
12.Click Evaluate Tasks.
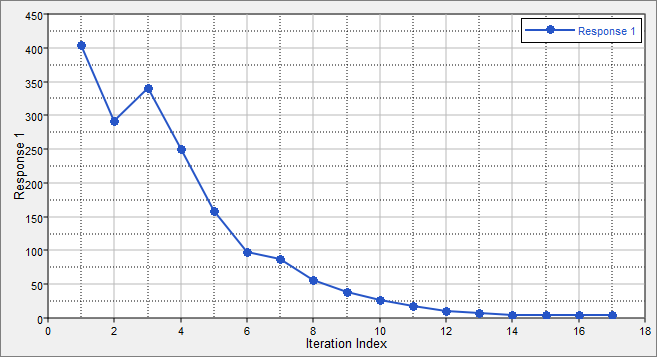
13.Optional. Click the Iteration Plot tab to monitor the progress of the optimization.

0050_final

 

 

 

See Also:

HyperStudy Tutorials