HyperStudy

HS-1705: Simple Fit Study

HS-1705: Simple Fit Study

 Previous topic Next topic Expand/collapse all hidden text  

HS-1705: Simple Fit Study

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

This tutorial demonstrates how to run a DOE study on simple functions defined using a Templex template.

The base input template defines two input variables; DV1 and DV2, labeled X and Y, respectively.  The objective of the study is to investigate the two input variables X, Y forming the two functions: X+Y and 1/X + 1/Y – 2.

Before running this tutorial, you must complete tutorial HS-1700: Simple DOE Study or you can import the archive file HS-1700.hstx, available in <hst.zip>/HS-1705/.

hmtoggle_plus1greyStep 1: Run a Space Filling DOE Study
1.In the Explorer, right-click and select Add Approach from the context menu.
2.In the HyperStudy - Add dialog, select Doe and click OK.
3.Go to the Specifications step.
4.In the work area, set the Mode to Hammersley.
5.Click Apply.
6.Go to the Evaluate step.
7.Click Evaluate Tasks. The evaluation results display in the work area.
8.Go to the Post processing step.
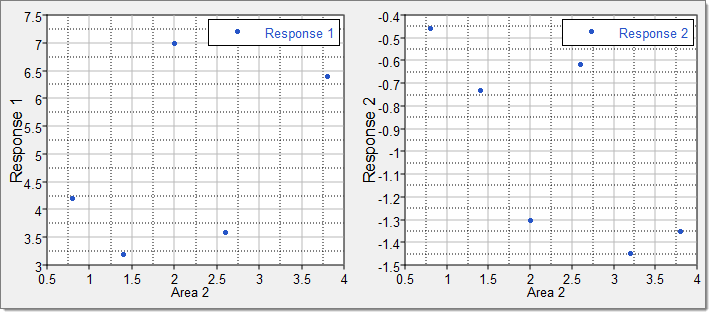
9.Click the Scatter 2D tab to view a plot which illustrates the dependency between Area 2 and Response 1 and Response 2.
a.Using the Channel selector, set the X Axis to Area 2 and the Y Axis to both Response 1 and Response 2.
b.Compare the scatter plots to determine if the runs are distributed homogeneously throughout the design space.

hs_1705_response 1

 
hmtoggle_plus1greyStep 2: Run a FIT Study
1.In the Explorer, right-click and select Add Approach from the context menu.
1.In the HyperStudy - Add dialog, select Fit and click OK.
2.Go to the Select matrices step.
3.Click Add Matrix.
4.In the HyperStudy - Add dialog, add one matrix.
5.In the work area, set Matrix Source to Doe 2 (doe_2).

hs_1705_import_matrix

6.Click Import Matrix.
7.Go to the Specifications step.
8.In the work area, set the Mode to Least Squares Regression (LSR).
9.Click Apply.
10.Go to the Evaluate step.
11.Click Evaluate Tasks.
12.Go to the Post processing step.
13.Click the Residuals tab to review the residuals of both output responses.

The data in the table shows the differences in the actual values and the predictions from the constructed Fit. The Percent Error column of Response_1 is numerically zero for all six runs; whereas the Percent Error column of Response_2 is up to 35%. The LSR fitting for Response_1 is acceptable, but the LSR fitting for Response_2 is rather large.

14.Click the Diagnostics tab to review the overall Fit quality.

Several measures are shown to indicate the relative quality of the Fit. The R-Square value can be interpreted as the percentage of variance in the data that can be explained by the Fit. For Response_1, the Fit captures 100% of the data variance; this makes sense as Response_1 is actually a linear function so the first order regression matches the actual data with no error. For Response_2, it is shown below that the Fit explains about 90% of the variance.

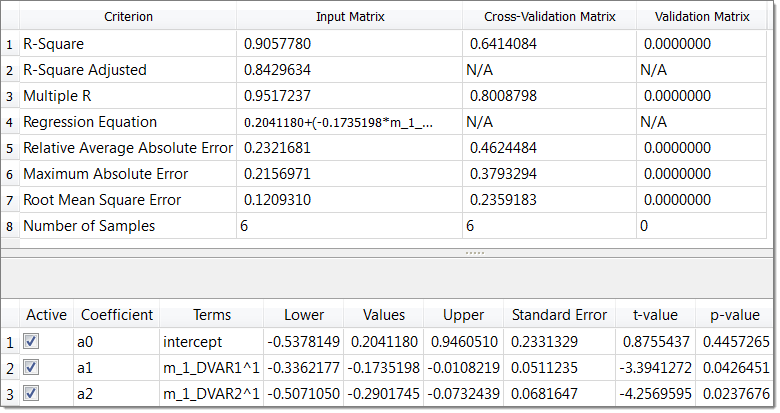
hs_1705_diagnostics

15.With first order least squares, you have a Fit which explains most of the data’s variance, but it still has a relatively high prediction error. Go back to the Specifications step and try different methods until you find an acceptable fitting for both output responses.

 

 

 

See Also:

HyperStudy Tutorials