Comparison of Results Obtained using Different Interfaces

---

Overview

---

The balls and the table have the same properties as previously defined. The dimensions of the table are 900 mm x 450 mm x 25 mm and the balls’ diameter is 50.8 mm.

Six interfaces are used to model the contacts (ball/ball and balls/table):

Table 2: Interfaces used in the problems.

The type 16 interface defines contact between a group of nodes (slaves) and a curved surface of quadratic elements (master part). The type 17 interface is used for modeling a surface-to-surface contact. For both interfaces, the Lagrange Multipliers method is used to apply the contact conditions; gaps are not required. Contact between the balls and the table is set as tied or sliding. Contact between the balls themselves is always considered as sliding. The type 7 interface enables the simulation of the most general contact types occurring between a master surface and a set of slave nodes. The Coulomb friction between surfaces is not modeled here (sliding contact) and the gap is fixed at 0.1 mm. The other parameters are set to default values.

The type 7 interface with the Penalty method is not available with 16-node thick shell elements. Thus, brick elements replace the 16-nodes shells in this case (check in the input file).

Contact modeling between balls (always sliding).

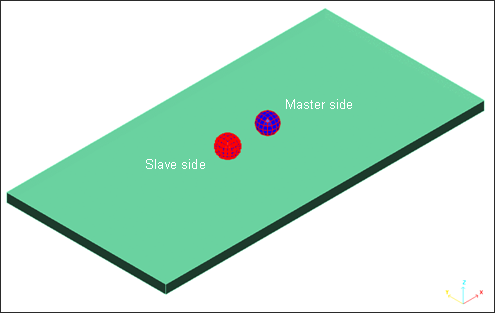
Fig 19: Definition of slave and master sides for contact.

The symmetrical interface definition is not recommended when using the Lagrange Multipliers method (types 16, 17 and 7-Lag). The problem using the interface with the Penalty method uses two interfaces to model the symmetrical impact.

Fig 20: Symmetrical configuration of the type 7 interface using the Penalty method

 

Contact between the balls and the table (sliding or tied depending on the problem):

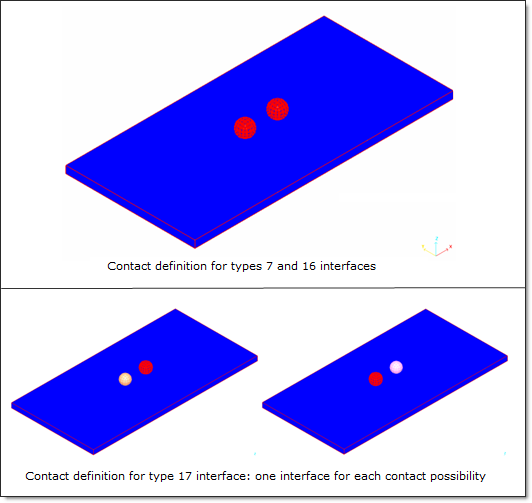
Fig 21: Definition of slave and master objects for balls/table contacts.

Pre-loading: quasi-static gravity loading to reach static equilibrium.

The explicit time integration scheme starts with nodal acceleration computation. It is efficient for the simulation of dynamic loadings. However, a quasi-static simulation via a dynamic resolution method needs to minimize the dynamic effects for converging towards static equilibrium and describes the pre-loading case before the dynamic analysis. Thus, the quasi-static solution of gravity loading on the model shows a steady state in the transient response.

To reduce the dynamic effect, dynamic relaxation can be used (/DYREL in the Engine file). A diagonal damping matrix proportional to the mass matrix is introduced into the dynamic equation:

with, being the relaxation value by default, equal to 1, and T being the period to be damped (less than or equal to the largest period of the system).

Thus, a viscous stress tensor is added to the stress tensor:

In an explicit code, the application of the dashpot force modifies the velocity equation:

without relaxation

 

with relaxation

with:

This option is activated in the Engine file (*_0001.rad) using /DYREL (inputs: = 1 and T = 0.2).

The dynamic problem (impact between balls) is considered in a second run managed by the second Engine file (*_0002.rad) with a time running from 30 ms to 130 ms.

Simulation Results: Kinetic Energy Transmission between Balls during Collision

---

Conclusion

---

A non-elastic collision appears using the type 7 interface Penalty method. After impact, each ball has about half of the initial velocity. The momentum transmission is partial and can be improved by increasing the stiffness of the interface despite the hourglass energy and degradation of the energy assessment.

Error on energy is more noticeable for interfaces using the Tied option, due to taking into account the rolling simulation.

This study shows the high sensitivity of the numerical algorithms for the modeling impact on elastic balls. Regarding the interface type, the kinematics of the problem and the transmission of momentum are more or less satisfactory. Type 16 interface allows good results to be obtained.