/ALE/GRID/STANDARD

Block Format Keyword

/ALE/GRID/STANDARD - Altair Grid Velocity Standard Formulation (2D and 3D)

Description

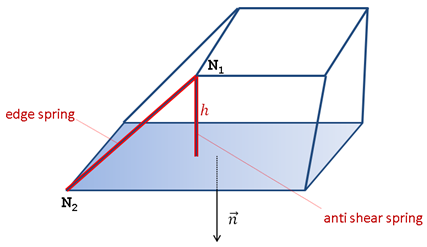
Describes the standard formulation for ALE grid velocity computation. It is an improved /ALE/GRID/SPRING formulation based on edge springs and anti-shear springs. (Comment 1)

ale_standard

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/ALE/GRID/STANDARD
						lc
Blank Format

Field	Contents
	Scale factor for maximum stiffness (Comment 2) = 1: critical stability stiffness limit at zero length. = 0: default value = 0.9 < 0: elastic forces on the element edges are set to 0. It gives more weight to anti-shear springs (auto-correction). (Real)
	Nonlinearity factor for edge spring stiffness (Comment 3) Default = 1e-2 (Real)
	Damping coefficient (Comment 4) Default = 1e-2 (Real)
lc	Characteristic length h < lc: Edge spring stiffness is increased h < lc / 5: Anti-shear spring is activated (Real)

1.	Fictitious springs are introduced on solid elements to control grid velocities.

These springs are nonlinear elastic viscous. To ensure stability, their stiffness is computed from time step. The two types of springs are edge and anti-shear springs.

Edge springs

The forces for an edge spring are a function of its length variation during time.

Where,

are grid velocities on nodes N1 and N2, respectively.

h is the N1 distance from opposite face

dt is the time step

and k(h) is the spring stiffness k(h) = kcritical

If h is inferior to the characteristic length lc and N1 is moving toward the opposite face then,

ale_standard_edgespring2

1/2 is the stability factor taking into account the damping factor , the scale factor , and time step dt (Comment 4).

ale_standard_towards

otherwise,

ale_standard_away

Anti-shear springs

The anti-shear forces are computed from node penetration. Gap is from opposite face.

and

ale_standard_critical

Viscous Damping

Viscous forces are computed from a critical damping corresponding to the upper bound for stiffness: 1/2

Grid Velocity

The grid velocity is then updated according to:

Where, m is fictitious mass on node from springs (automatically computed during Starter).

2.	Increasing = 1, the maximum stiffness will be increased. The scale factor determines the maximum stiffness for a given spring at zero length. The scale factor ensures that the critical stability value is not exceeded (to avoid time step decrease).

This flag is acting on stiffness shape. Stiffness is linear with

= 0. Moreover, increasing

, the lower bound stiffness for edge spring will be increased. Springs have a critical stiffness at zero length (this corresponds to a unitary factor). For a length greater than or equal to the characteristic length, the spring stiffness is the critical stiffness multiplied by

4.	It is recommended to use small values for , otherwise damping may become over critical. The stability factor is:

5.	All these parameters can be modified during an Engine restart (/ALE/GRID/STANDARD).

6.	Mesh auto correction. It is possible to give more weight to anti-shear forces by either:

•	Setting lc parameter close to the mesh size

•	Setting a negative value for parameter (elastic forces on edges are set to 0 at the first cycle of current run)

7.	This method assumes a homogeneous spring repartition around each node. This is not the case when connecting two meshes, where topologies are different.