CMBEAM

Bulk Data Entry

CMBEAM – Beam Element for MBD

Description

Defines a beam element for multi-body dynamics solution sequence without reference to a property entry.

Format

Field	Contents
EID	Unique element identification number. (Integer > 0)
MID	Material identification number. Only MAT1 material definitions may be referenced by this element. (Integer > 0)
GA, GB	Grid point identification number of connection points. (Integer > 0; GA ≠ GB)
X1, Y1, Z1	Components of vector v at end A, measured at end A, parallel to the components of the displacement coordinate system for GA, to determine (with the vector from end A to end B) the orientation of the element coordinate system for the BEAM element. (Real)
G0	Grid point identification number to optionally supply X1, X2, and X3 (Integer > 0). Direction of orientation vector is GA to G0. (Integer > 0)
L	Undeformed length along the X-axis of the beam. (Real)
A	Area of the beam cross-section. No default (Real > 0.0)
I1	Area moment inertia in plane 1 about the neutral axis. No default (Real > 0.0)
I2	Area moment inertia in plane 2 about the neutral axis. No default (Real > 0.0)
J	Torsional constant. (Real > 0.0)
K1, K2	Area factor for shear. Default = 0.0 (Real)

1.	The X-axis of the beam is always along the line connecting G1 and G2. The Z-axis of the beam is determined based on the X-axis and the Y-axis provided by G3/X1, Y1, and Z1.

2.	The moments of inertia are defined as follows:

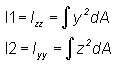
cmbeam_eq

The beam coordinates must be aligned with the principal axes of the cross-section.

3.	The transverse shear stiffness in planes 1 and 2 are (K1)AG and (K2)AG, respectively. If a value of 0.0 is used for K1 and K2, the transverse shear flexibilities are set to 0.0 (K1 and K2 are interpreted as infinite).

4.	This card is represented as a bar2 element in HyperMesh.