Convergence Enhancement for the ESLM

It is important to catch the critical responses of a structure properly when optimizing the structure. Generally, it is a good practice to define many time steps in the time intervals where the critical responses of interest show up. By doing this, the optimizer can consider more precise responses at the critical time intervals, resulting in a decreased probability that the optimizer will go in the wrong direction in the current outer loop.

Here is an example that shows how to refine specific time intervals. Suppose the analysis time interval is from 0 seconds to 1.0 seconds. In order to find out at which steps the critical responses of interest show up, you could use equi-spaced time steps first.

MBSIM 4 TRANS END 1.0 NSTEPS 100

The above card divides the time interval from 0 seconds to 1.0 seconds into 100 time steps, which is an equi-spaced time step. After analyzing with the above card, the following time history for stress can be obtained: At the time interval of around 0 seconds to 0.02 seconds and 0.60 seconds to 0.63 seconds, critical values of the stress show up. Generally speaking, these critical responses are dominant responses that control the optimization process. It is desirable to consider more critical responses at around these time intervals. In order to consider more critical responses at around these time intervals, increase the number of times steps at these time intervals.

$more time steps from 0.0 sec to 0.02 sec.

MBSIM 1 TRANS END 0.02 NSTEPS 200

+ VSTIFF

MBSIM 2 TRANS END 0.61 NSTEPS 200

+ VSTIFF

$more time steps from 0.61 sec to 0.63 sec.

MBSIM 3 TRANS END 0.63 NSTEPS 200

+ VSTIFF

MBSIM 4 TRANS END 1.0 NSTEPS 100

MBSEQ 10 1 2 3 4

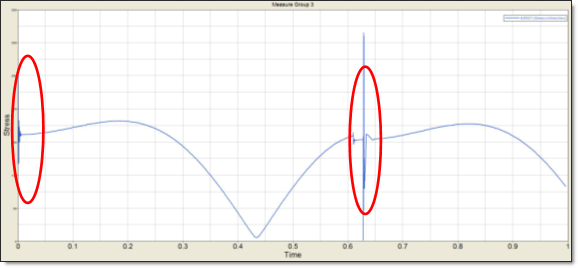
time_hist

Time history of a response

In the above MBSIM cards, time steps in the time interval 0 to 0.02 seconds and the time interval 0.61 and 0.63 seconds have been increased. Generally, the more information the optimizer is provided, the better the solution it can provide. It is beneficial to define many time steps; enough to catch precisely the critical responses in the time intervals where critical response of interest show up. This will enhance convergence of the optimization process.