Equivalent Static Load Method (ESLM) |

|

|

|

|
|
Equivalent Static Load Method (ESLM) |

|

|

|

|
The equivalent static load method, originally published by Dr. Park, Hanyang University, is a technique suitable for optimization of designs undergoing dynamic loads. The method has been implemented for the optimization of the following solutions:
| • | Multi-body dynamics problems including flexible bodies |
| • | Nonlinear responses from implicit static analysis, implicit dynamic analysis and explicit dynamic analysis |
The equivalent static load method takes advantage of the well established static response optimization capabilities of OptiStruct.
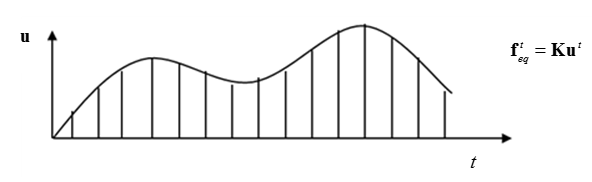
Figure 1.1: Displacement – time history response
The equivalent static load is that load which creates the same response field as that of the dynamic/nonlinear analysis at a given time step. From Figure 1.1, an equivalent static load is calculated corresponding to each time step in the time history of the solution, thereby replicating the dynamic/nonlinear behavior of the system in a static environment.
The calculated equivalent static loads from the analysis (as explained above) are considered as separate load cases, and these multiple load cases are used in the linear response optimization loop. An updated design from the optimization loop is then passed back to the analysis for validation and overall convergence. The design is validated against the original dynamic/nonlinear analysis. Based on the outcome of this validation, the solution converges or an updated set of equivalent static loads is calculated for the updated geometry, and the entire process is repeated till convergence. Figure 1.2 is a graphic description of the equivalent static load method for optimization.
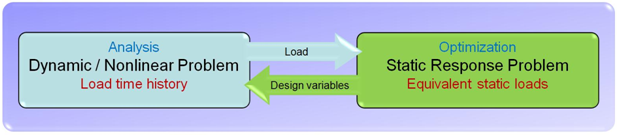
Figure 1.2: Equivalent static load method
The equivalent static load method is completely automated in OptiStruct and is an efficient approach for the optimization of responses from transient, dynamic and nonlinear solutions.
Apart from others, the equivalent static load method offers the following benefits:
| • | It can be applied at the concept design phase as well as design fine tuning phase, i.e. it can be used with topology, free-sizing, topography, size, shape and free-shape optimization. |
| • | A design is optimized for updated loads, due to an updated design during the optimization process. |
ESL optimization is considered to be converged, if one or more of the following conditions is met:
| • | There is no change in both the objective function value and in the maximum constraint violation between two outer loops. |
| • | There is no improvement in both the objective and in the maximum constraint violation between to outer loops. |
| • | The previous six objective function values oscillated around the optimum. |