The cyclical pattern grouping allows you to force OptiStruct to create a series of symmetric shape variables about a central axis that repeat a number of times determined by you (with the UCYC field). This can be useful in assigning a reinforcement pattern in a circular plate that matches an angularly repeated load in a symmetric fashion.

For cyclical pattern groupings (TYP = 40 and 41), OptiStruct generates a series of symmetric shape variables about an axis defined by the cross product of the first and second vectors. The axis of rotation is positioned at the anchor point. The first vector defines a plane establishing one side of the cyclical wedge. The other side of the cyclical wedge is defined by the angle of repetition. The figure below shows cyclical pattern grouping for three "wedges".

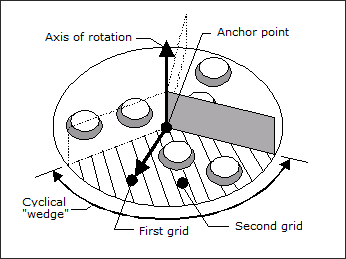
TYP = 40: Cyclical pattern grouping for 3 repetitions

OptiStruct allows any number of repeated cyclical wedges by entering the number of desired wedges into field 30 (UCYC). OptiStruct internally calculates the repetition angle according to the formula 360.0/UCYC. For example, setting UCYC to three results in three wedges of 120.0 each, and setting UCYC to 6 results in six wedges of 60.0 each.

You can also control whether the cyclical repetitions will be symmetric within themselves. This is done by choosing one of the cyclical TYP options ending in ‘1’ (41, 51, 61, 71, and 81). If the symmetric wedge option is selected, OptiStruct will force each wedge to be symmetric about its centerline. Selecting one of the cyclical options ending in ‘0’ (40, 50, 60, 70, and 80) will result in the wedges being non-symmetric. See the figures below:

Other Forms of Cyclical Pattern Grouping

OptiStruct supports the combination of cyclical pattern grouping with one plane symmetry, linear pattern grouping, radial pattern grouping, and radial linear pattern grouping. Each option is specified with a different base TYP number to which the number denoting the repetition angle is added.

For one plane cyclical pattern grouping (TYP = 50 and 51), the cyclical patterns are reflected about a plane located at the anchor node and defined by the cross product of the first and second vectors. One plane cyclical symmetry ensures that nodes equal distances above and below the plane of symmetry will be grouped into the same variables. See below:

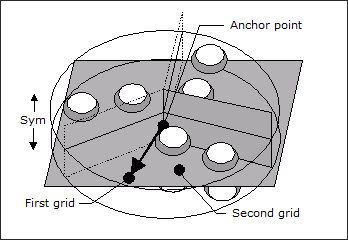
TYP = 50: One plane cyclical symmetry with 3 wedges

For linear cyclical symmetry (TYP = 60 and 61), OptiStruct generates shape variables that run along a line parallel to the cross product of the first and second vectors. These shape variables have a width equal to the minimum bead width parameter but have no limit on length. The full lengths of the linearly drawn shape variables will be cyclically symmetric:

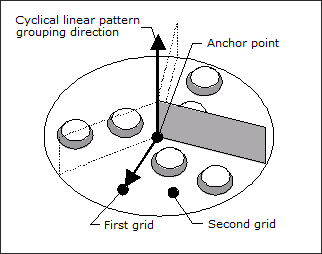
TYP = 60: Linear cyclical pattern grouping with 3 wedges

For radial cyclical pattern grouping (TYP = 70 and 71), OptiStruct generates shape variables that run radially away from a central axis defined by the cross product of the first and second vector. Radial beads have a width equal to the minimum bead width parameter but have no limit on length. The width of the beads does not change depending on the distance from the center. The full lengths of the radially drawn shape variables will be cyclically symmetric:

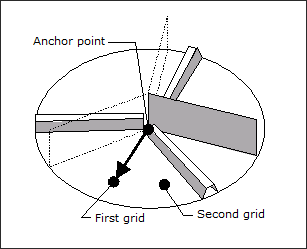
TYP = 70: Radial cyclical pattern grouping with 3 wedges

For radial linear cyclical pattern grouping (TYP = 80 and 81), OptiStruct generates a series of planes that run radially away from and in the same plane as the first vector. The radial linear cyclical pattern grouping is essentially the linear cyclical pattern grouping combined with the radial pattern grouping. The full lengths of the radially drawn shape variables will be cyclically symmetric.