NOLIN3

Bulk Data Entry

NOLIN1 – Nonlinear Transient Load as a Positive Variable Raised to a Power

Description

Defines nonlinear transient forcing functions of the form

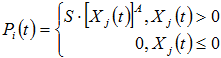
nolin3_1

where, Xj(t) may be a displacement or a velocity at point GJ in the direction of CJ.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
NOLIN3	SID	GI	CI	S	GJ	CJ	A

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
NOLIN3	4	102		-6.1	2	15	-3.5

Field

Contents

SID

Nonlinear load set identification number.

No default (Integer > 0)

Grid or scalar point identification number at which nonlinear load is to be applied.

No default (Integer > 0)

Component number for GI.

No default (1 < Integer < 6; blank or 0, if GI is a scalar point)

Scale factor.

No default (Real)

Grid or scalar point identification number.

No default (Integer > 0)

Component number for GJ, GK according to the following table:

Type	Displacement	Velocity
Grid	1 < Integer < 6	11 < Integer < 16
Scalar	Blank or 0	Integer = 10

Exponent of the forcing function.

No default (Real)

1.	Nonlinear loads must be selected by the Subcase Information data selector NONLINEAR.

2.	Nonlinear loads may not be referenced on a DLOAD entry.

3.	All degrees-of-freedom referenced on NOLIN3 entries must be members of the solution set.

4.	Nonlinear loads may be a function of displacement or velocity . Velocities are denoted by components ten greater than the actual component number; that is the component 11 indicates velocity in the 1 component direction. The velocity is determined by:

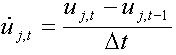
nolin1_5

where, is the time step interval and is the displacement of GJ-CJ for the previous time step.

5.	Use a NOLIN4 entry for the negative range of Xj(t) .

6.	The time step algorithm in transient solution sequences may loose unconditional stability when this load entry is used. In most practical cases, the time step size chosen to reach a certain accuracy is below the stability limit. It is recommended to decrease the time step if results diverge.