Reliability-based Design Optimization (Beta) |

|

|

|

|
|
Reliability-based Design Optimization (Beta) |

|

|

|

|
Reliability-based Design Optimization (RBDO) is an optimization method that can be used to provide optimum designs in the presence of uncertainty. A gradient-based local approximation of responses is used to perform reliability analysis. The design variables, constraints, and objective are tested for reliability based on user-defined reliability requirements.
Deterministic and Random design variables can be selected for a design optimization run, while a Random parameter is also available to check for Robustness of a particular design within specified bounds. Similarly, Design Constraints and Objectives can also be specified as Deterministic (mean) or Percentile values.
The Single Loop Approach (SLA) is used to optimize structures using Reliability-based Design Optimization in OptiStruct. Reliability-based optimization methods test the reliability of designs for each optimization iteration. The traditional, double-loop RBDO algorithm requires nested optimization loops, where the design optimization (outer) loop repeatedly calls a series of reliability (inner) loops.
The computational time can be prohibitive for practical problems due to the nested optimization-reliability loops. The SLA converts the nested loops into a single loop using Karush-Kuhn-Tucker (KKT) conditions of the inner reliability loops in the outer optimization loop. The probabilistic optimization problem is converted into a deterministic optimization problem. SLA is highly efficient compared to the traditional double-loop RBDO process.
The Single Loop Approach (SLA) is terminated if one of the following conditions is met:
| 1. | The Sequential Quadratic Programming (SQP) convergence criterion is achieved. |
| 2. | Design variable convergence criterion is achieved. |
| 3. | Maximum number of allowable iterations is attained. |
The following design variables and parameters can be used to define the structural design space in OptiStruct:
Random Design Variables
Random design variables are defined via the RAND continuation lines on the DESVAR bulk data entry. Various random distribution types can be selected and their parameters are defined accordingly. In an RBDO process, during reliability and/or robustness analysis, the design should satisfy optimality based on the specified distributions.
Random parameters
The definition of Random parameters is similar to that of Random Design Variables, using RANP definition. However, the important difference is that, while the mean values of random variables are changed to improve the design, the mean values of random parameters remain constant. For example, typically sheet metal thickness can be a random variable, due to fabrication variance, while the Young’s modulus of a material would typically be a random parameter, if its variance is accounted for.
Deterministic Design Variables
The deterministic design variables are the regular design variables used in an OptiStruct optimization run.
|
The following design objective types are available in OptiStruct:
Percentile value (RBDO)
The minimum or maximum of the percentile based objective function can be defined on the DESOBJ subcase information entry. The MINP/MAXP options and the PROB argument can be used to define the required parameters.
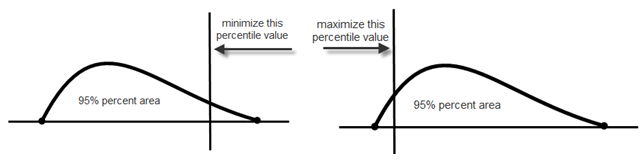
Figure 1: Illustration depicting Percentile Value based Objective
The percentile value based objective is defined as follows:
![]() or
or ![]()
Where, ![]() is the objective function, and r is the probability level (for example, 95%). The right and left percentile values are available. MINP minimizes the right percentile value and MAXP maximizes the left percentile value.
is the objective function, and r is the probability level (for example, 95%). The right and left percentile values are available. MINP minimizes the right percentile value and MAXP maximizes the left percentile value.
Deterministic (mean) value
The deterministic value based objective is the regular objective used in an OptiStruct optimization run. The mean value based objective is defined as follows:
![]() or
or ![]()
Where, ![]() is the objective function.
is the objective function.
The following design constraint types are available in OptiStruct:
Percentile value (RBDO)
The probability of one constraint satisfying its bounds should not be less than the predefined reliability value. The reliability value is defined via the PROB field on the DCONSTR bulk data entry.
The reliability-based constraints are defined as follows:
![]()
![]()
Where, ![]() is the constraint value, UB is the upper bound of the constraint, LB is the lower bound of the constraint, and r is the probability level (for example, 95%).
is the constraint value, UB is the upper bound of the constraint, LB is the lower bound of the constraint, and r is the probability level (for example, 95%).
For the ![]() constraint, the right percentile value of
constraint, the right percentile value of ![]() is forced to be less than or equal to the upper bound UB. For the
is forced to be less than or equal to the upper bound UB. For the ![]() constraint, the left percentile value of
constraint, the left percentile value of ![]() is forced to be greater than or equal to the lower bound LB.
is forced to be greater than or equal to the lower bound LB.
Deterministic (mean) value
The deterministic value based constraint is the regular constraint definition used in an OptiStruct optimization run. The mean value based constraint is defined as follows:
![]()
![]()
Where, ![]() is the constraint value, UB is the upper bound of the constraint, and LB is the lower bound of the constraint.
is the constraint value, UB is the upper bound of the constraint, and LB is the lower bound of the constraint.
The RBDO process is illustrated in Figure 2.
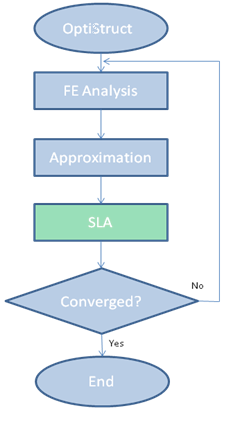
Figure 2: Flowchart depicting the OptiStruct RBDO implementation
Note that while all deterministic optimization capabilities in OptiStruct use the same approximation approach, design requirements are accurately evaluated after each FEA analysis. This premise does not hold for RBDO as accurate reliability analysis would need more FEA analyses for a given design. Therefore, it is important to assess the usability of the implemented algorithm. Seventeen examples are tested to verify the reliability of this approach. In these examples, distribution types of random design variables are normal distribution and constraints have a reliability requirement of 99%. A Monte Carlo simulation with 1000 sampling points based on accurate FEA analysis is used to check the reliability status (Table 1).
Example |
NME |
Start Design Status |
Optimized Design Status |
||||
|---|---|---|---|---|---|---|---|
T |
N |
M |
Objective |
Reliability |
Objective |
Reliability |
|
1 |
5 |
28 |
3 |
40.4 |
98.0% |
27.6 |
98.5% |
2 |
2 |
26 |
7 |
4.51 |
0.0% |
3.24 |
100.0% |
3 |
3 |
4 |
4 |
3.84e-5 |
70.4% |
3.99e-5 |
98.8% |
4 |
4 |
159 |
5 |
9.0e-4 |
100.0% |
4.47e-4 |
98.9% |
5 |
3 |
2 |
4 |
1.98 |
0.0% |
0.472 |
98.1% |
6 |
3 |
4 |
13 |
0.5 |
0.0% |
2.98e-4 |
99.0% |
7 |
2 |
20 |
8 |
4.83 |
100.0% |
3.41 |
98.8% |
8 |
8 |
170 |
13 |
661.4 |
0.0% |
552.8 |
98.5% |
9 |
3 |
316 |
8 |
5.785 |
0.0% |
6.825 |
98.8% |
10 |
2 |
1 |
6 |
26.07 |
100.0% |
21.03 |
100.0% |
11 |
8 |
2 |
7 |
3.9e-5 |
0.0% |
1.229e-4 |
99.0% |
12 |
6 |
16 |
8 |
0.01 |
0.0% |
3.45e-3 |
96.4% |
13 |
2 |
3 |
8 |
232.4 |
0.0% |
240.1 |
100.0% |
14 |
5 |
3 |
4 |
40.0 |
0.0% |
39.3 |
98.1% |
15 |
10 |
168 |
3 |
49.4 |
100.0% |
71.9 |
97.3% |
16 |
3 |
22 |
11 |
4.83 |
0.0% |
2.70 |
98.8% |
17 |
2 |
1060 |
6 |
232.5 |
0.0% |
61.5 |
100.0% |
T: test number of the example
N: number of random design variables
M: number of reliability constraints
NME: number of model evaluations
Objective: the objective value of the design; in these examples, objective value is to be minimized
Reliability: the probability of the design that satisfies the constraint requirement
The following conclusions can be drawn from the results in Table 1:
| 1. | The OptiStruct RBDO approach is very efficient, since it consumes just a few model evaluations. |
| 2. | The reliability of the optimized design is close to the predefined requirement in most cases. Error does exist, however, and can be quite significant as observed in examples 12 and 15. |
The OptiStruct RBDO approach (based on local approximation) offers an efficient tool to consider uncertainty involved in design. For most problems this approximate reliability analysis yields reasonable estimates. Local approximation based reliability analysis does, however, contain some error of varying degree. Accurate reliability analysis should be carried out if accurate satisfaction of reliability requirements is critical. Also note that for the approximation-based OptiStruct RBDO approach, reliability analysis is performed only for retained constraints for which sensitivity is available. The screening criteria can be adjusted with the DSCREEN bulk data entry, if required.