DESVAR (Bulk Data Entry)

Bulk Data Entry

DESVAR – Design Variable

Description

Defines a design variable.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
DESVAR	ID	LABEL	XINIT	XLB	XUB	DELXV	DDVAL
+	RAND	ITYPE	P1	P2	P3
+	RANP	ITYPE	P1	P2	P3

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
DESVAR	1	DV001	0.0	-1.0	1.0

Field	Contents
ID	Unique design variable identification number. (Integer > 0)
LABEL	User-defined name for the variable. LABEL must begin with an alphabetical character, and cannot have embedded blanks. (Character)
XINIT	Initial value for variable. (Real between XLB and XUB)
XLB	Design variable lower bound. (Real)
XUB	Design variable upper bound. (Real)
DELXV	Initial move limit for each design variable. (Real > 0.0 or blank) Size: fraction of the variable itself. (Default = value of DOPTPRM parameter DELSIZ) Shape: fraction of the range (XUB – XLB) of the variable. (Default = value of DOPTPRM parameter DELSHP)
DDVAL	ID of DDVAL entry that provides a set of discrete values. (Blank or Integer > 0; Default = blank for continuous design variables)
RAND	Random Design Variable Indicates that the random design variable distribution parameters for Reliability-based Design Optimization (RBDO) are to follow.
ITYPE	Type of Random Distribution (Comments 4, 5, and 6): (Character string) NORM – Normal distribution LOG – Logarithmic normal distribution UNIF – Uniform distribution TRIA – Triangular distribution EXPO – Exponential distribution WEIB – Weibull distribution
P1	The first distribution parameter (Comments 4, 5, and 6) Default = 0.0 (Real)
P2	The second distribution parameter (Comments 4, 5, and 6) Default = 0.0 (Real)
P3	The third distribution parameter (Comments 4, 5, and 6) Default = 0.0 (Real)
RANP	Random parameter Indicates that the random parameter distribution parameters for Reliability-based Design Optimization (RBDO).

Comments

1.	Only the initial value of the move limits can be set. Move limits are automatically adjusted to enhance iterative stability and convergence speed.

2.	If the design variable is discrete (Integer > 0 in DDVAL field), and if either XLB and/or XUB bounds are wider than those given by the discrete list of values on the corresponding DDVAL entry, XLB and/or XUB will be replaced by the minimum and maximum discrete values.

3.	Setting XINIT=XLB=XUB freezes the design variable.

4.	The various distribution types are as follows:

Normal Distribution (ITYPE = NORM):

The normal distribution is one of the most important continuous distributions in nature. It approximates the probability of a random distribution of phenomena that fall between two real numbers.

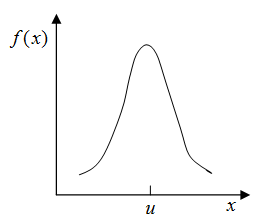
distribution_norm_graph

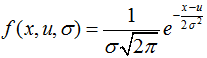
distribution_norm

Where, u is the mean and is the standard deviation.

In OptiStruct RBDO, the normal distribution can be defined as on the corresponding fields in the DESVAR entry.

Log-normal Distribution (ITYPE = LOG):

The log-normal distribution is a continuous probability function which approximates the distribution of a random variable whose logarithm is normally distributed. The log-normal distribution is often used in risk analyses.

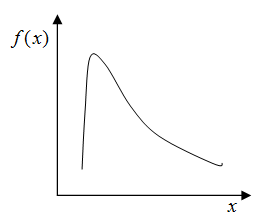
distribution_log_graph

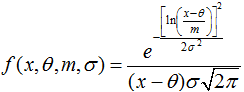
distribution_log

Where, . is the shape parameter and is also the standard deviation of the log of the distribution; is the location parameter and is the scale parameter and is also the median of the distribution.

In OptiStruct RBDO, the log-normal distribution can be defined as on the corresponding fields in the DESVAR entry.

Uniform distribution (ITYPE = UNIF):

The uniform distribution is a continuous probability function which approximates the distribution of a random variable between a minimum and maximum when all values are equally likely (such as from a random generator).

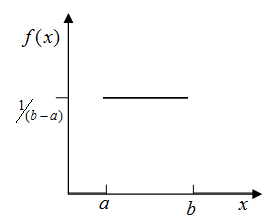
distribution_unif_graph

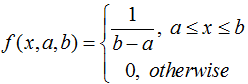
distribution_unif

Where, a < b , a and b are end points.

In OptiStruct RBDO, the uniform distribution can be defined as on the corresponding fields in the DESVAR entry.

Triangular distribution (ITYPE = TRIA):

The Triangular distribution is used when the only info known is the minimum, the most likely value, and the maximum.

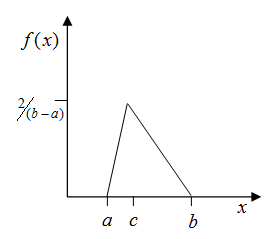
distribution_tria_graph

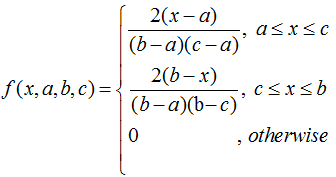
distribution_tria

Where, a, b, and c are end points and the mode.

In OptiStruct RBDO, the triangular distribution can be defined as on the corresponding fields in the DESVAR entry.

Exponential distribution (ITYPE = EXPO):

The Exponential distribution describes the amount of time between events, and the mean time between failures.

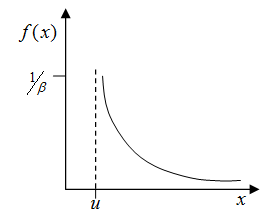
distribution_expo_graph

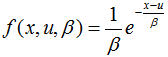
distribution_expo

Where, is the location parameter, is the scale parameter.

In OptiStruct RBDO, the exponential distribution can be defined as on the corresponding fields in the DESVAR entry.

Weibull distribution (ITYPE = WEIB):

The Exponential distribution describes the amount of time between events, and the mean time between failures.

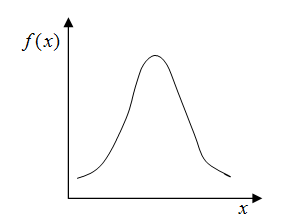
distribution_weib_graph

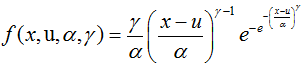
distribution_weib

Where, is the shape parameter; u is the location parameter and is the scale parameter.

In OptiStruct RBDO, the Weibull distribution can be defined as on the corresponding fields in the DESVAR entry.

Due to the deviation of the random distribution, the design region needs to be defined carefully. For example, if a design variable value is intended to be positive, then its lower bound should not be defined lower than n*

; where,

is the standard deviation of the variable; n is a constant multiplier (a value of n=6 is recommended). This applies, in a similar fashion, to the upper bound.

The three distribution parameters, P1, P2, and P3 determine the various distribution curves. As the mean value of the design variable will change during the optimization process, the corresponding distribution parameter will be updated accordingly. This means that the distribution curve moves while the shape does not change. For instance, for Normal Distribution (ITYPE=NORM), the first parameter is the mean and therefore, has no influence on Reliability-based Design Optimization. The DESVAR directly defines the mean value of the random variable/parameter. Therefore, for some distribution types, P1 can be set to 0.0 and OptiStruct will automatically calculate the values. These distribution types include, Normal, Lognormal, Exponential, and Weibull distributions.

7.	This card is represented as an optimization designvariable in HyperMesh