MotionView User's Guide

Bushings Panel - Trans and Rot Stiffness Tabs

Bushings Panel - Trans and Rot Stiffness Tabs

 Previous topic Next topic Expand/collapse all hidden text  

Bushings Panel - Trans and Rot Stiffness Tabs

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

The Trans Stiffness and Rot Stiffness tabs allow you to define the stiffness properties of a compliant joint or a bushing.  Stiffness can be linear or non-linear.

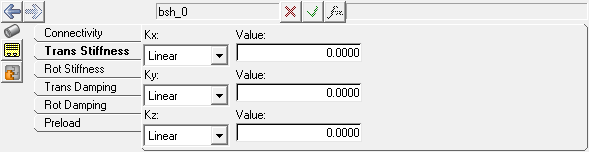
bushing-stiffness

Bushings panel - Trans Stiffness tab

For:

Enter:

Kx, Ky, Kz Linear

translational stiffness coefficient in the local x, y, z direction.

Kx, Ky, Kz Curve

force transmitted through the bushing, expressed in the form of a force vs. displacement curve that is a function of a set of independent variables.

Select AKIMA, CUBIC, or LINEAR under Interpolation and enter a value under Independent variable.  Resolve the curve by clicking Curve and selecting a curve from the Select a Curve dialog.

Kx, Ky, Kz Spline3D

select AKIMA, CUBIC, LINEAR, or QUINTIC under Interpolation and specify an expression each under Independent variable X and Independent variable Z.  Resolve the 3D spline by clicking on the Spline3D collector and selecting a Spline3D entity from the Select a Spline3D dialog.

Kx, Ky, Kz Expression

force transmitted through the bushing, expressed in the form of a function expression.

Ktx Kty, Ktz Linear

rotational stiffness coefficient in the local x, y, z direction.

Ktx, Kty, Ktz Curve

torque transmitted through the bushing, expressed in the form of a torque vs. displacement curve that is a function of a set of independent variables.

Select AKIMA, CUBIC, or LINEAR under Interpolation and enter a value under Independent variable.  Resolve the curve by clicking Curve and selecting a curve from the Select a Curve dialog.

Ktx, Kty, Ktz Spline3D

select AKIMA, CUBIC, LINEAR, or QUINTIC under Interpolation and specify an expression each under Independent variable X and Independent variable Z.  Resolve the 3D spline by clicking on the Spline3D collector and selecting a Spline3D entity from the Select a Spline3D dialog.

Ktx, Kty, Ktz Expression

torque transmitted through the bushing, expressed in the form of a function expression.

Non-linear stiffness properties can be defined using curves, user-defined properties, or expressions.

hmtoggle_plus1To define non-linear properties:
1.Select Linear from the Property drop-down menu.
2.Enter a function expression containing a formula in the Value text box that defines the non-linear property.
hmtoggle_plus1To define non-linear properties using expressions:
1.Select Expression from the Property drop-down menu.
2.Enter a function expression containing a formula in the Expression text box that defines the non-linear property.

 

How do I...

Defining Non-linear Properties Using Curves