MotionView User's Guide

MV-1080: Creating an Analysis using MDL

MV-1080: Creating an Analysis using MDL

 Previous topic Next topic No expanding text in this topic  

MV-1080: Creating an Analysis using MDL

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

In this tutorial, you will learn how to create an analysis definition and instantiate it in an MDL file.

An analysis is a collection of loads, motions, output requests, and entities (bodies, joints, etc.) describing a particular event applied to a model.  For example, an analysis to determine the kinematics of a four-bar mechanism can be described in one analysis, while another analysis can be used to study a dynamic behavior.  In both cases, while the overall model is the same, the analysis container may contain different entities that form the event.  The kinematic analysis can contain motion and related outputs, while the dynamic analysis may contain forces and its corresponding outputs.

•An analysis definition is similar to a system definition in syntax and usage, except:
oAnalysis definitions use *DefineAnalysis(), while system definitions use *DefineSystem().
oAnalysis can be instantiated under the top level Model only.
oOnly one analysis can be active in the model at a given instance.
•A analysis definition block begins with *DefineAnalysis() and ends with *EndDefine().  All entities defined within this block are considered to be part of the analysis definition.

The syntax of *DefineAnalysis() is as follows:

*DefineAnalysis(ana_def_name,  arg_1,arg_2, ..., arg_n)

Where;

-ana_def_name is the variable name of the analysis definition and will be used while instantiating the analysis.
-arg_1,arg_2..arg_n are a list of arguments passed to the analysis definition as attachments.
•The following table illustrates an analysis definition and its subsequent instantiation within an MDL file.  Two files, an analysis definition file and the model file, work together when instantiating a particular analysis under study.  Some of the terms in the example below are in bold to highlight a few key relationships between the files.

Reference Numbers

System Instantiation with Definition

1

// Model : Body.mdl

*BeginMDL(base_model, "Base Model")

2

//Instantiate the analysis definition ana_def

*Analysis(ana1, "Analysis 1", ana_def, j_rev)

3

//Begin Analysis Defintion Block

*DefineAnalysis(ana_def,j_joint_att)

4

//Declare a joint attachment to the analysis

*Attachment(j__joint_att, "Joint Attachment", Joint, "Add an joint external to this analysis to apply motion/force")

5

//Entities within the analysis

*Point(p_1, "Point in the analysis")

*Body(b_1, "Body in the analysis")

6

//Define a joint with the body b_sys and the body attachment b_att

*Motion(mot, "Joint Motion", JOINT, j_joint_att, ROT)

7

*EndDefine()  //End Definition Block

8

*EndMDL()
•The following table details the relationships between the analysis definition and its instantiation in the MDL Model file.

Variable

Relationship

j_joint_att

The varname of the attachment, declared in the *Attachment() statement (line 4) in the analysis definition file, appears as an argument in the *DefineAnalysis() statement (line 3). A motion is applied on this joint using the *Motion() statement (line 6).

ana_def

The varname of the analysis definition is specified in the *DefineAnalysis() statement (line 3).  The analysis definition is used by ana1 in the *Analysis() statement (line 2).

Defining relationships between the analysis definition and MDL model files

Exercise: Creating an Analysis Definition

An experimental technique for estimating the natural frequencies of structures is to measure the response to an impulsive force or torque, then look at the response in the frequency domain via a Fourier Transform.  The peaks in the frequency response indicate the natural frequencies.  In this tutorial, we will create an analysis to simulate this test procedure.  The analysis applies an impulsive torque to the system and measures the response.

1.Use the following function expression to create the impulse torque about the x axis.

Tx = step(TIME,.3, 0, .31, 10) + step(TIME, .31, 0, .32, -10)

2.Apply this torque to estimate the natural frequencies of the triple pendulum model shown in the image below:

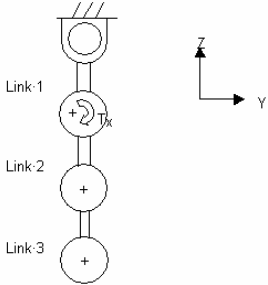
mv-1080-01

Schematic representation of a triple pendulum in stable equilibrium

Your analysis applies to a pendulum with any number of links or to more general systems.

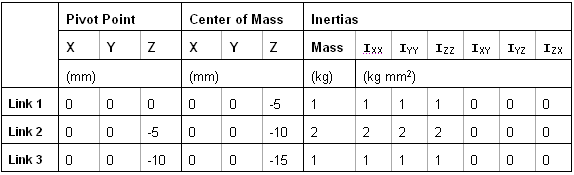
mv-1080-table2

Properties table for the triple pendulum

The following MDL statements are used in this exercise:

*Attachment()

*ActionReactionForce()

*SetForce()

*Output()

NoteRefer to the MotionView Reference Guide (located in the HyperWorks Desktop Reference Guide) for the syntax of the above MDL statements.

Step 1: Create the analysis definition file.

1.Open an empty file in a text editor.
2.Create the *DefineAnalysis() and *EndDefine() block.  All other statements will be added between this block.
•In the text editor, define an analysis with a variable name of def_ana_0 and one argument j_att as an attachment.

*DefineAnalysis(def_ana_0, j_att)

3.The torque may be applied between two bodies connected by a revolute joint, with the origin of the revolute joint taken as the point of application of the force. This allows you to have only one attachment; the revolute joint.
•Create an *Attachment() statement which defines j_att as the attachment and Joint as the entity type.  Make sure that the variable name used in the statement is the same as is used in the *DefineAnalysis() statement.

*Attachment(j_att, “Joint Attachment”, Joint, “Select joint to apply torque”)

4.Use the *ActionReactionForce() statement to define an applied torque.  Please note to reference the correct properties of the attachment joint to reach the bodies involved in the joint.

Note

Refer to the description of the dot separator in MDL. You can access properties of an entity by using the dot separator.

For example, bodies attached to the revolute joint can be accessed as:
<joint variable name>.b1 and as <joint variable name>.b2.
•Create an *ActionReactionForce() statement with the following:
-Variable name of force_1.
-Force type as ROT (rotational).
-Body 1 as j_att.b1 (attachment joint body 1).
-Body 2 as j_att.b2 (attachment joint body 2).
-Force application point as j_att_i.origin (the attachment joint origin).
-Reference frame as Global_Frame (global).

*ActionReactionForce( force_1, "Torque", ROT, j_att.b1, j_att.b2, j_att.origin, Global_Frame )

5.Use the *SetForce() statement to set the value to the force defined in the previous step.
•Create a *SetForce() statement with a variable name of force_1 (the existing force) and the following torque values:

TX = step(TIME,.3,0,.31,10) + step(TIME,.31,0,.32,-10),TY = 0,TZ = 0

6.Use an *Output() statement to output the applied force.
•Define an *Output() statement with the following:
-Variable name of o_force.
-Output type as FORCE.
-Entity type as FORCE.
-Variable name of force_1 (the action-reaction force created in Step 3 above).
-Reference frame as Global_Frame (global).

*Output( o_force, "Input Torque", FORCE, FORCE, force_1, Global_Frame)

7.Save the analysis definition as analysis.mdl.

The saved file analysis.mdl will look like this:

*DefineAnalysis( def_ana_0,j_att )

*Attachment(j_att, “Joint Attachment”, Joint, “Select joint to apply torque”)

 

*ActionReactionForce( force_1, "Torque", ROT, j_att.b1, j_att.b2, j_att.origin,  Global_Frame )

 

*SetForce( force_1, EXPR, `step(TIME,.3,0,.31,10) + step(TIME,.31,0,.32,-10)`)

 

*Output( o_force, "Input Torque", FORCE, FORCE, force_1, Global_Frame)

*EndDefine()

Step 2: Instantiate the analysis in a model.

1.Start MotionView and open the triplependulum.mdl file, located in the mdl folder.
2.From the Project Browser, click Model.

The Systems/Assembly panel is displayed.

3.Click the Import/Export tab.
4.Using the Select File: file browser mv-tut_folder_icon, pick the analysis definition you just created, analysis.mdl.
5.Click Import.
6.Make sure that the Select a definition drop-down menu is set to Analysis.

mv-1080-one

7.Click OK.
8.Select the newly added analysis by clicking on Analysis 0 in the Project Browser, and resolve the joint attachment by selecting any one of the pivot joints of the triple pendulum:
-From the Attachments tab, select the Joint Attachment.
-Select any pivot joint of the triple pendulum.

mv-1080-two

9.Save your model as new_triplependulum.mdl.
10.Solve the model.  From the Main tab of the Run panel run-24, specify the End time as 1.0 and the Print interval as 0.01.
11.View the animation animationStart-24.
12.Plot the output "Input Torque" using the .abf file from the solution.