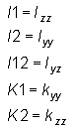Cross Sectional Properties Calculated by HyperBeam |

|

|

|

|
|
Cross Sectional Properties Calculated by HyperBeam |

|

|

|

|
Cross Sectional Properties Calculated by HyperBeam |

|

|

|

|
|
Cross Sectional Properties Calculated by HyperBeam |

|

|

|

|
The beam cross section is always defined in a y,z plane. The x-axis is defined along the beam axis. The coordinate system you define is called the local coordinate system; the system parallel to the local coordinate system with the origin in the centroid is called the centroidal coordinate system; the system referring to the principal bending axes is called the principal coordinate system.
For shell sections, only the theory of thin walled bars is used. This means that for the calculation of the moments and product of inertia, terms of higher order of the shell thickness t are neglected. Thickness warping is also neglected.
Area |
|
||
|
|||
Area Moments of Inertia |
|
||
|
|||
|
|||
Area Product of Inertia |
|
||
|
|||
Radius of Gyration |
|
||
|
|||
Elastic Section Modulus |
|
||
|
|||
|
|||
Max Coordinate Extension |
|
||
|
|||
Plastic Section Modulus |
|
||
|
|||
|
|||
Torsional Constant |
Solid |
(see below for warping function) |
|
Shell open |
|
||
Shell closed |
|
||
|
|
||
Elastic Torsion Modulus |
Solid |
|
|
Shell open |
|
||
Shell closed |
|
||
|
|
||
Shear Center |
|
||
|
|||
Warping Constant (normalized to the shear center) |
|
||
|
|
||
Shear deformation coefficients |
|
||
|
|||
|
|||
|
|||
Shear stiffness factors |
|
||
|
|||
|
|||
|
|||
Shear stiffness |
|
||
Warping Function |
For solid sections, the warping function is computed using a finite element formulation. This may lead to un-physically high stresses in geometric singularities (sharp corners) that get worse with mesh refinement. This may cause problems computing the elastic torsion modulus. |
||