22.2 - Ditching using ALE (Mono-Domain) |

|

|

|

|
|
22.2 - Ditching using ALE (Mono-Domain) |

|

|

|

|
TitleDitching using ALE (Mono-Doman) |
|
||||
Number22.2 |
|||||
Brief DescriptionImpact of a simple object on water simulated by ALE approach. |
|||||
Keywords
|
|||||
RADIOSS Options |
|||||
Compared to / Validation Method
|
|||||
Input File<install_directory>/demos/hwsolvers/radioss/22_Ditching/Ditching_Mono_Domain_ALE/* |
|||||
Technical / Theoretical Level Skilled |
|||||
The problem consists of a simple object falling into water simulating the ditching of a helicopter.
Units: mm, ms, KN, GPa, kg.
Impact of a triangular object on water is performed and the results are compared qualitatively [2], also using the experimental data obtained from the Politechnico di Milano [1].
The computation is performed using several impact velocities of 3.5 and 11 m/s.
The material used for the object follows a linear elastic law (/MAT/LAW1) with the following characteristics:
| • | Initial density: 7.8 x 10-6 kg.mm-3 |
| • | Young modulus: 206.9 GPa |
| • | Poisson ratio: 0.3 |
The material law for water is BIPHAS law (/MAT/LAW37) with the following characteristics:
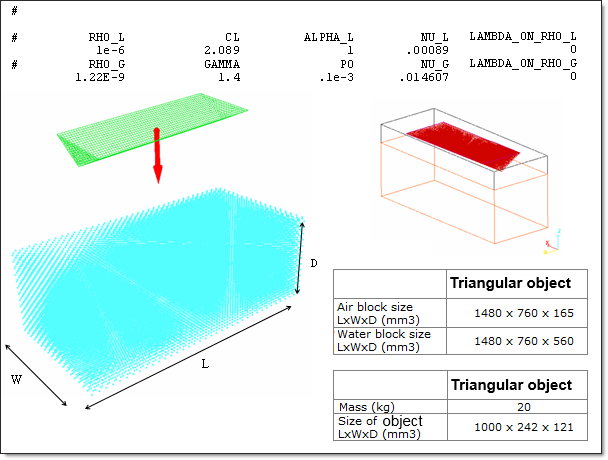
Fig 1: Problem data.
The object is modeled using shell elements with an average mesh size of 15 x 15 mm2. In order to simplify the computation, it is put in a rigid body with an accelerometer on the master node.
The water is modeled using 15x15x15 mm mesh with a total of 166023 elements. The material law BIPHAS (/MAT/LAW37) is used.
The air is modeled using a BIPHAS material with the following characteristics:
#blank
# RHO_L CL ALPHA_L NU_L LAMBDA_ON_RHO_L
1e-6 2.089 0 .00089 0
# RHO_G GAMMA P0 NU_G LAMBDA_ON_RHO_G
1.22E-9 1.4 .1e-3 .014607 0
The boundary conditions are applied to the pool as following:
| • | Z displacement component fixed for lower and upper faces |
| • | Y displacement component fixed for lateral faces normal to Y |
| • | X displacement component fixed for lateral faces normal to X |
An interface type 18 is defined to manage the contact between the solid in Lagrangian mesh (Prism) and the fluid (pool). The diedra is defined as master and the nodes in the pool (air and water) as slave.
The interface type 18 forces are computed by Penalty method. The interface stiffness is proportional to impact velocity. The results obtained by the ALE approach can be highly dependent to the interface stiffness factor Stfac, which should be adjusted in function of size of element and fluid properties.
The interface type 18 forces are computed by Penalty method. The forces are proportional to the stiffness factor Stfac which should be calibrated. The following graph shows the dependence of results (acceleration at the accelerometer) to the mesh and Stfac.
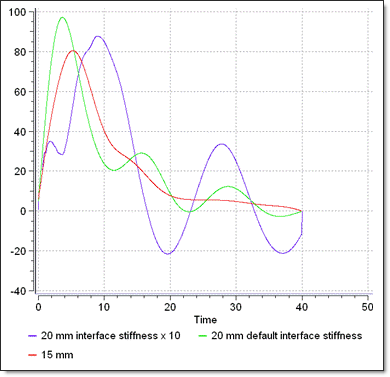
Fig 2: Higher peak force with coarse mesh and interface stiffness dependence
Higher peak forces are obtained with the coarse mesh. That can be partially corrected by filtering, as shown in Fig 3.
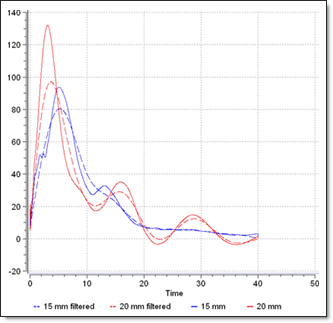
Fig 3: Filtering of results for coarse and fine meshes
Using a filter CFC 60, -3 dB, the simulation results of the ALE and SPH approaches are compared to Von Karman theoretical solution and experimental measures in Fig 4.
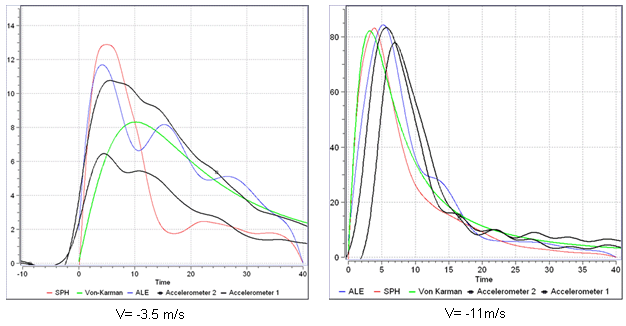
Fig 4: Comparison between simulation results, theoretical solution and experimental measures (acceleration)
SPH and ALE approaches respectively give the maximum acceleration of 83g and 84g. However, the Von Karman theory delivers 82g; with the maximum value by experience is between 83g and 73g.
On the other hand, the duration for acceleration beyond 40g is respectively 7.9ms and 8.2ms for SPH and ALE simulation methods, where the experience provides values between 7.5ms and 8.5ms and the Von Karman theory provides 8 ms.
Note that:
| • | The computation time is similar for both SPH and ALE approaches. |
| • | Using a fine enough mesh, both RADIOSS methods SPH and ALE provide satisfactory results, compared to experience and analytical solution. |
| • | The ALE approach is more robust and stable when the SPH signal is highly vibrated. |
| • | The use of a coarse mesh in the ALE approach requires the interfaced stiffness calibration. |
[1] CAST Deliverable 5.5.1 Generic Water Impact Tests performed at Politecnico di Milano (Polytechnic University of Milan).
[2] Olivier Pastore Study and modelization of rigid bodies impact during sea landing phase; Annex 1 Von Karman's Theoretical Models, T. Miloh et al. May.