Iform = 11

Block Format Keyword

/MAT/LAW51 - Iform = 11: Generic Multi-material law with up to 3 Elasto-plastic Materials and one high explosive. Yield criteria type can be defined for each material.

Description

Able to handle up to four materials:

•	Three elasto-plastic materials with polynomial EOS, following the available yield criteria: Johnson-Cook or Drücker-Prager

•	One high explosive material with JWL EOS

The sub-material boundaries inside an element are not explicitly defined, but an anti-diffusive technique is used to avoid expansion of transition zone (Comment 1).

Compatible only with 3D analysis and EULER or ALE formulation.

LAW51 is based on equilibrium between each materials present inside the element. RADIOSS computes and outputs a relative pressure . At each cycle:

= 1 = 2 = 3= 4

Total pressure can be calculated with external pressure:

Where, P is positive for a compression and negative for traction.

Hydrostatic stresses are computed from Polynomial EOS:

Where, which means that EOS is linear for an expansion and cubic for a compression.

By default, the process is adiabatic Q = 0. To enable thermal computation, refer to Comment 6.

Deviatoric stresses can be computed with either Johnson-Cook model or Drücker-Prager:

Johnson-Cook:

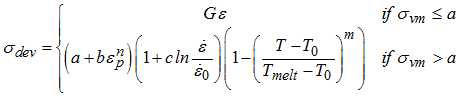
Drücker-Prager:

J2 = (A0 + A1P + A2P2)

High explosive material is modeled with linear EOS if unreacted (for equilibrium purpose) and JWL EOS for detonation products:

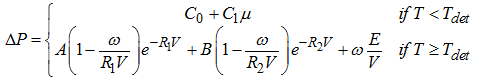
Where, V is relative volume: V = Volume / V0 and E is the internal energy per unit initial volume: E = Eint / V0. For more details, refer to Comments 9 to 13.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/MAT/LAW51/mat_ID
mat_title
Blank Format
Iform			Ipla_1	Ipla_2	Ipla_3
#Global parameters
Pext
#SubMaterial_1 parameters
(Input depends on Ipla_1 flag, see below)
#SubMaterial_2 parameters
(Input depends on Ipla_2 flag, see below)
#SubMaterial_3 parameters
(Input depends on Ipla_3 flag, see below)
#SubMaterial_4 parameters (Necessarily Jones-Wilkins-Lee material law)

A		B		R1		R2
D		PCJ						IBFRAC

Specific input for sub-material j (j= 1, 2, or 3) parameters:

If Ipla_j = 0 (no Yield criteria) sub-material input:

If Ipla_j = 1 (Johnson-Cook Yield criteria) sub-material input

If Ipla_j = 2 (Drücker-Prager yield criteria) sub-material input:

Field	Contents	SI Unit Example
mat_ID	Material identifier (Integer, maximum 10 digits)
mat_title	Material title (Character, maximum 100 characters)
Iform	Formulation flag (Integer)
Ipla_j	Yield criteria flag (sub-material index j could be 1, 2, or 3) (Integer) = 0: no yield criteria (default) = 1: Johnson-Cook = 2: Drücker-Prager
#Global parameters
Pext	External pressure (Comment 2) Default = 0 (Real)
	Global Kinematic viscosity (shear) (Comment 3) Default = 0 (Real)
	Global Kinematic viscosity (volumetric) (Comment 3) Default = 0 (Real) (Stokes Hypothesis)
#submaterial parameters for Polynomial EOS
	Initial volumetric fraction (Comment 4) (Real)
	Initial density (Real)
	Initial energy per unit volume (Real)
	Hydrodynamic cavitation pressure (Comment 5) Default = -10-30 (Real)
	Initial pressure (Real)
	Hydrodynamic coefficient (Real)
	Hydrodynamic coefficient (Real)
	Hydrodynamic coefficient (Real)
	Hydrodynamic coefficient (Real)
	Hydrodynamic coefficient (Real)
	Elasticity shear modulus (Real)
#submaterial parameters specific to Johnson-Cook yield criteria
	Plasticity yield stress (Real)
	Plasticity hardening parameter (Real)
	Plasticity hardening exponent Default = 1.0 (Real)
	Strain rate coefficient Default = 0.00 (Real) = 0: no strain rate effect
	Reference strain rate (Real) If means no strain rate effect
	Temperature exponent (Real) = 0: no temperature effect
#submaterial parameters specific to thermal behavior
	Initial temperature Default = 300 K (Real)
	Melting temperature Default = 1030 (Real)
	Maximum temperature Default = 1030 (Real)
	Specific heat per unit of volume (Comment 7) (Real)
	Failure plastic strain Default = 1030 (Real)
	Plasticity maximum stress Default = 1030 (Real)
	Thermal conductivity coefficient 1 (Comment 8) (Real)
	Thermal conductivity coefficient 2 (Comment 8) (Real)
#submaterial parameters specific to Drücker-Prager criteria
	Young Modulus (Real)
	Poisson’s ratio (Real)
	Yield coefficient (Real)
	Yield coefficient (Real)
	Yield coefficient (Real)
	Yield coefficient (Real)
#submaterial parameters specific to Jones-Wilkins-Lee EOS
	Initial volumetric fraction of unreacted explosive (Comment 4) (Real)
	Initial density of unreacted explosive (Real)
	Detonation energy (Real)
	Minimum pressure (Comment 5) Default = -10-30 (Real)
	Initial pressure of unreacted explosive (Real)
A	JWL EOS coefficient (Real)
B	JWL EOS coefficient (Real)
R1	JWL EOS coefficient (Real)
R2	JWL EOS coefficient (Real)
	JWL EOS coefficient (Real)
D	Detonation velocity
PCJ	Chapman-Jouget pressure (Real)
	Bulk modulus for unreacted explosive (Comment 8) (Real)
IBFRAC	Burn fraction calculation flag (Comment 11) (Integer) = 0: Volumetric Compression + Burning Time = 1: Volumetric Compression only = 2: Burning Time only

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

/MAT/LAW51/1

Underground explosion in Calcareous Soil - UNITS {g,cm,µs}

#---------------------------------------------------------------------------------------------------

# Material Law No 51. ALE MULTI-MATERIAL SOLID LIQUID GAS

#---------------------------------------------------------------------------------------------------

# RHO_I RHO_0

# IFLG IPLA_1 IPLA_2 IPLA_3

11 2 0 1

# P_EXT NU LAMDA

0 0 0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#---Plastic material with Drucker-Prager Yield Criteria--------------------------------------------#

# ALPHA_1 RHO_0_1 E_0_1 P_MIN_1 C_0_1

1.0 2.33 0 -1E-20 1E-6

# C_1_1 C_2_1 C_3_1

0.256 0.256 1

# A0_1 A1_1 A2_1 A_MAX_1

.670000030E-12 .940000010E-06 .330000010 .000000000

# E_1 NU_1

0.45220 .28

# T_10 T_1MELT T_1LIMIT RHOCV_1

0 0 0 0

# EPSILON_MAX_1 SIGMA_MAX_1 K_A_1 K_B_1

0 0 0 0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#---Gas with PerfectGas EOS------------------------------------------------------------------------#

# ALPHA_2 RHO_0_2 E_0_2 P_MIN_2 C_0_2

0.0 .0013 2.5E-6 -1E-20 0

# C_1_2 C_2_2 C_3_2 C_4_2 C_5_2

0 0 0 .4 .4

# G_2

# T_20 T_2MELT T_2LIMIT RHOCV_2

0 0 0 0

# EPSILON_MAX_2 SIGMA_MAX_2 K_A_2 K_B_2

0 0 0 0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#---Plastic material with Johnson-Cook Yield criteria----------------------------------------------#

# ALPHA_3 RHO_0_3 E_0_3 P_MIN_3 C_0_3

0.0 0 0 0 0

# C_1_3 C_2_3 C_3_3 C_4_3 C_5_3

0 0 0 0 0

# G_3 SIGMA_Y_3 BB_3 N_3

0 0 0 0

# CC_3 EPSILON_DOT_0_3

0 0

# CM_3 T_30 T_3MELT T_3LIMIT RHOCV_3

0 0 0 0 0

# EPSILON_MAX_3 SIGMA_MAX_3 K_A_3 K_B_3

0 0 0 0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#---High Explosive with Jones-Wilkins-Lee EOS------------------------------------------------------#

# ALPHA_4 RHO_0_4 E_0_4 P_MIN_4 C_0_4

0.0 1.60 .07 -1E-20 1e-6

# B_1 B_2 R_1 R_2 W

3.7100 .03231 4.15 .95 .3

# D P_CJ C_14 I_BFRAC

.693 .21 .04 0

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

#---Defining LAW #1 as ALE material law------------------------------------------------------------#

/ALE/MAT/1

# Modif. factor.

#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

1.	The anti-diffusive technique can be adjusted with /UPWIND from Starter Input. The 3 flag is the upwind coefficient for a damp area:

: Full Upwind (default, recommended value)

: Zero Upwind (less diffusive, but potentially unstable)

2.	RADIOSS computes and outputs a relative pressure .

However, total pressure is essential for energy integration (dEint = -PdV). It can be computed with the external pressure flag Pext.

P = + Pext leads to dEint = -(Pext + ) dV.

This means if Pext = 0, the computed pressure is also the total pressure = P.

3.	Kinematic viscosities are global and not specific to each material for computing viscous stress tensor:

Where, is the dynamic shear viscosity flag, and

is the dynamic volumetric viscosity flag.

4.	Volumetric fractions enable sharing of elementary volume within the three different materials.

For each material, must be defined between 0 and 1.

Sum of initial volumetric fractions must be equal to 1.

For automatic initial fraction of the volume, refer to the /INIVOL card.

5.	flag is the minimum value for the computed pressure . It means that total pressure is also bounded to:

For fluid materials and detonation products must remain positive to avoid any tensile strength, so must be set to -Pext.

For solid materials, default value is suitable but may be modified.

6.	Heat contribution is computed only if the thermal card is associated to the material law (/HEAT/MAT).

In this case , and the parameters for thermal diffusion are read for each material:

, , and

For solids and liquids, and for perfect gas .

7.	The temperature evolution in the Johnson-Cook model is computed with the flag , even if the thermal card (/HEAT/MAT) is not defined.

8.	Thermal conductivity, K, is linearly dependent on the temperature:

K(T) = KA + KBT

9.	It is highly recommended to provide a strictly positive coefficient for unreacted explosive EOS in order to ensure equilibrium calculation and numerical stability.

If this value is unknown, a stable and acceptable value is:

Where, is the clarity of the sound in water (SI:1500m/s).

10.	Explosive material ignition is made with detonator cards, refer to /DFS/DETPOIN or /DFS/DETPLAN.

11.	Detonation Velocity (D) and Chapman Jouget Pressure (PCJ ) are used to compute the burn fraction calculation (). It controls the release of detonation energy and corresponds to a factor which multiplies JWL pressure.

For a given time: P(V,E) = Bfrac Pjwl (V,E)

A detonation time Tdet is computed by the Starter from the detonation velocity. During the simulation the burn fraction is computed as follows:

where, the burn fraction calculation from burning time is:

and the burn fraction calculation from volumetric compression is:

It can take several cycles for the burn fraction to reach its maximum value of 1.00.

Burn fraction calculation can be changed defining the IBFRAC flag:

IBFRAC = 1: $law5_Ibfrac1_eq$

IBFRAC = 2: $law5_Ibfrac2_eq$

As of version 11.0.240, Time Histories for Detonation time and burn fraction are available through /TH/BRIC with BFRAC keyword. This allows to output a function f whose first value is detonation time (with opposite sign) and positive values corresponds to the burn fraction evolution.

dfs_detpoin_eq

12.	Detonation times can be written in the Starter listing file for each JWL element. The printout flag (Ipri) must be greater than or equal to 3 (/IOFLAG).