|
»Click here to display Table of Contents«
|
Contact Treatment |
|
|
|
|
|
Contact Treatment |
|
|
|
|
|
»Click here to display Table of Contents«
|
Contact Treatment |
|
|
|
|
|
Contact Treatment |
|
|
|
|
There are two approaches that deal with contact:
| • | Penalty method: The most commonly used in explicit codes and can be found in most of the RADIOSS interfaces |
| • | Lagrange Multiplier method: Used in special case studies |
Interfaces using the penalty method are based on master/slave treatment. Contact can only occur between a set of slave nodes and a set of master segments. Master segments are defined depending on the type of element they lie on. If it is a 3-node or a 4-node shell, the segment is the surface of the element. If it is a solid element, the segment is defined as a face. Finally, if it is a 2D solid element (quad), the segment is a side.
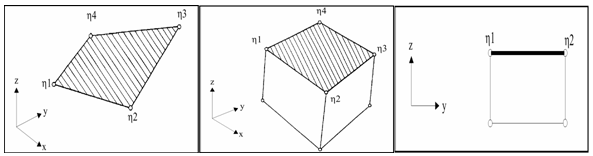
Fig. 5.1: Segment definition
A gap distance is defined to determine whether or not a node is in contact with a segment.
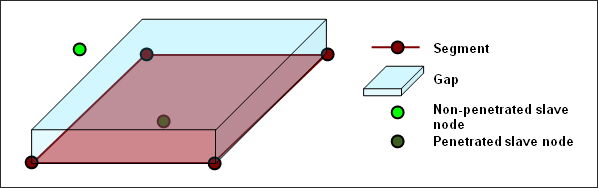
Fig. 5.2: Gap and penetration
As soon as a node penetrates into the gap, an elastic spring is added between the slave node and the master segment. Therefore, a resistant force will tend to reject the slave node.
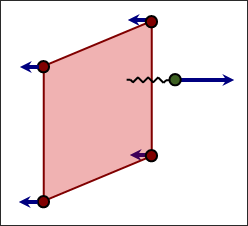
Fig. 5.3: Reaction force in interface
The time step may be affected by the interface stiffness. During the penetration, as a spring is connected to the slave node, the spring stiffness must be added to the overall stiffness acting on the node (stiffness from all elements connected to this node). The nodal time step must be reduced to account for the spring stiffness.
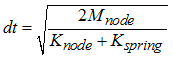
Contact ends when the penetrated node is completely pushed out of the gap. Therefore, the elastic spring and the reaction force are removed.
It is worthwhile to note that the contact interfaces with penalty method are fully compatible will all kinematic conditions (for example, rigid body, imposed velocity, etc.).
Contrary to the penalty method, the Lagrange Multiplier method is purely mathematical and does not require physical elements (springs) to model contact. A nonlinear system of equations is solved to account for contact conditions. Therefore, there is no time step collapse due to high interface stiffness, but it takes more CPU time to do one cycle as new equations need to be solved by a nonlinear solver. The method has the advantage to stop slave nodes at the contact surface (the contact condition is precisely satisfied); however the friction cannot be computed.