HyperWorks Solvers

Example 5 - Beam Frame

Example 5 - Beam Frame

 Previous topic Next topic No expanding text in this topic  

Example 5 - Beam Frame

 Previous topic Next topic JavaScript is required for expanding text JavaScript is required for the print function  

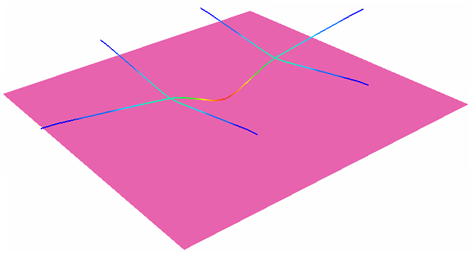
rad_ex_5_beam

Summary

A beam frame with clamped extremities receives an impact at its mid-point from a pointed mass having initial velocity. The material is subjected to the elasto-plastic law of Johnson-Cook. The model is meshed with beam elements. An infinite rigid wall with only one slave node, including the impacted node, is subjected to the initial velocity. This example is considered a dynamic problem and the explicit solver is used.

The explicit approach leads to finding a quasi-static equilibrium of the structure after impact.

Title

Beam-frame

rad_ex_5.1

Number

5.1

Brief Description

A beam frame receives an impact from a mass having initial velocity.

Keywords

•Beam
•Rigid wall
•Plasticity and Johnson-Cook material (/MAT/LAW2)

RADIOSS Options

•Boundary conditions (/BCS)
•Initial velocities (/INIVEL)
•Beam element (/PROP/BEAM)
•Rigid wall (/RWALL)

Input File

Beam_frame: <install_directory>/demos/hwsolvers/radioss/05_Beam-frame/FRAME*

Technical / Theoretical Level

Beginner

Overview

Aim of the Problem

The purpose of this example is to perform a static analysis using beam elements.

Physical Problem Description

A pointed mass (3 kg) makes an impact at point O of a beam frame (see Fig 1 for the geometry) using a speed of 10 ms-1 in the Z direction. The beams are made of steel and each beam section is square-shaped (each side being 6 mm long).

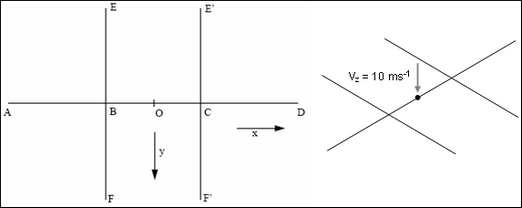
rad_ex_fig_5-1

Fig 1: Geometry of the frame.

Dimensions are: AB = BC = CD = BE = BF = E’C = CF’ = 90 mm.

Points A, D, E, F, E’, and F’ are fixed.

The beams have the following properties:

•Cross section: 36 mm2
•Moments of inertia in Y and Z: 108 mm4
•Moments of inertia in X : 216 mm4

The steel material used has the following properties:

•Density: 0.0078 g/mm3
•Young’s modulus: 200 000 MPa
•Poisson’s ratio: 0.3
•Yield stress: 320 MPa
•Hardening parameter: 134.65 MPa
•Hardening exponent: 1.0

All other coefficients are set to default values. Plasticity is taken into account using Law 2 without failure.

Analysis, Assumptions and Modeling Description

Modeling Methodology

The mesh is a regular beam mesh, each beam being 9 mm long (total = 70 beams).

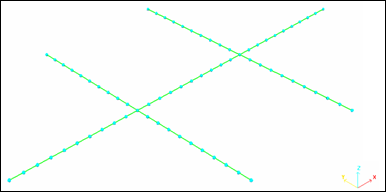
rad_ex_fig_5-2

Fig 2: Mesh of the frame showing the position of the nodes.

RADIOSS Options Used

The impacting mass is simulated using a sliding rigid plane wall (/RWALL) having an initial velocity of 10 ms-1 and a mass of 3000 g. Only one slave node exists: the node O to simulate a point impact.

Points A, F, F', D, E and E' are fully fixed.

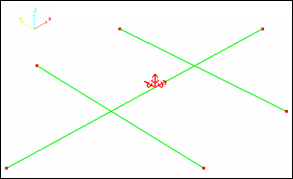
rad_ex_fig_5-3        rad_ex_fig_5-4

Fig 3: Boundary conditionsFig 4: Rigid wall type infinite plane

Simulation Results and Conclusions

Curves and Animations

The main results refer to the time history of points B and O with regard to displacements and velocities.

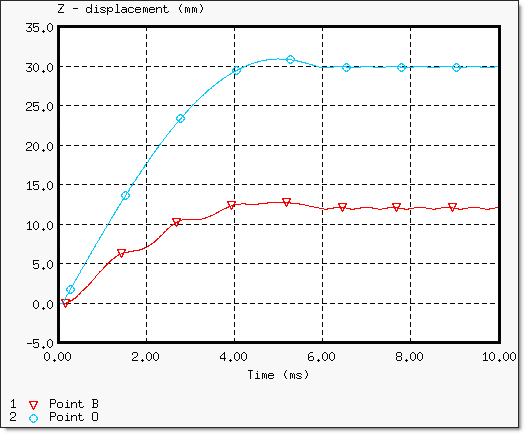
rad_ex_fig_5-5

Fig 5: Displacements of points B and O.

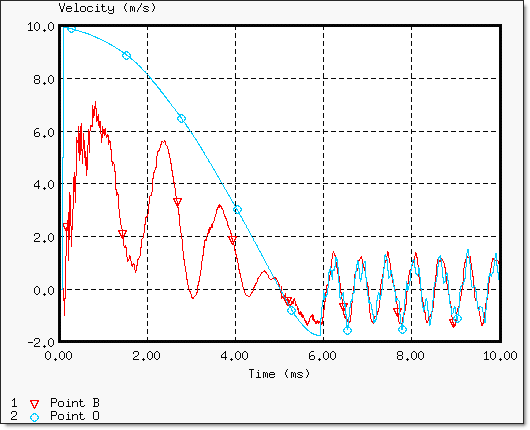
rad_ex_fig_5-6

Fig 6: Velocity of points B and O (stabilization).

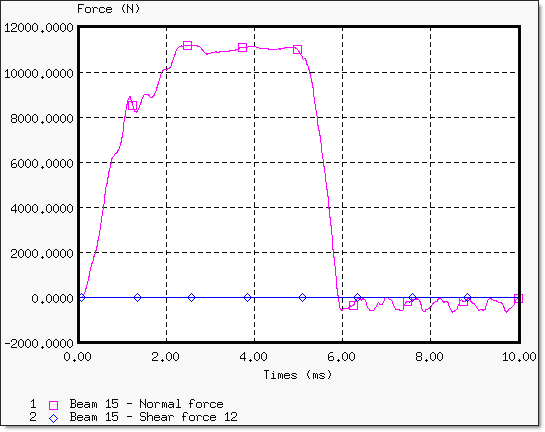
rad_ex_fig_5-7

Fig 7: Normal and shear force on beam element 15 (near to point O).

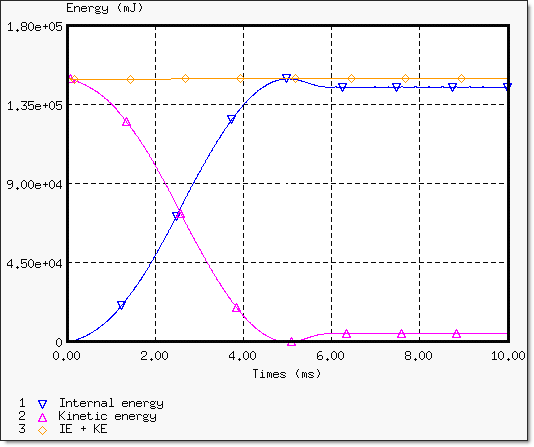
rad_ex_fig_5-8

Fig 8: Energy assessment (stability reached at in 6 ms).

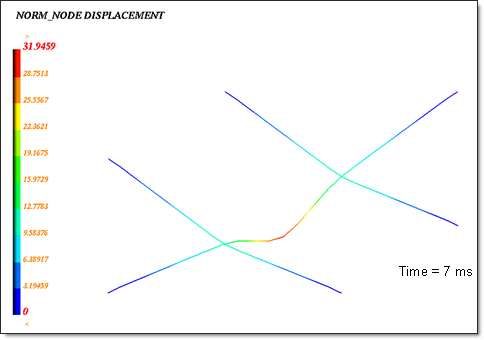
rad_ex_fig_5-9

Fig 9: Node displacement (max. = 30.96 mm).

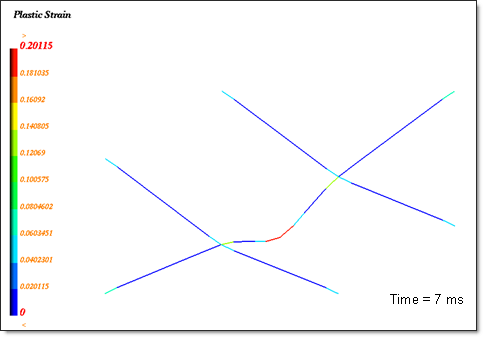
rad_ex_fig_5-10

Fig 10: Plastic strain (max. = 20.1%).