Block Format Keyword
/RWALL - Rigid Walls
Description
Defines the following types of rigid walls: Infinite Plane, Infinite Cylinder, Sphere and Parallelogram.
Format
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
/RWALL/type/rwall_ID/unit_ID
|
rwall_title
|
node_ID
|
Slide
|
grnd_ID1
|
grnd_ID2
|
|
|
|
|
|
|
Dsearch
|
fric
|
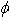
|
ffac
|
ifq
|
|
If node_ID = 0
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
XM
|
YM
|
ZM
|
|
|
|
|
If node_ID ≠ 0
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
Mass
|
VX0
|
VY0
|
VZ0
|
|
|
If type is Plane, Cyl, Paral.
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
XM1
|
YM1
|
ZM1
|
|
|
|
|
If type is Paral.
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
(8)
|
(9)
|
(10)
|
XM2
|
YM2
|
ZM2
|
|
|
|
|
|
Field
|
Contents
|
SI Unit Example
|
type
|
Rigid wall type keyword
(see table below)
|
|
rwall_ID
|
Rigid wall identifier
(Integer, maximum 10 digits)
|
|
unit_ID
|
Optional unit identifier
(Integer, maximum 10 digits)
|
|
rwall_title
|
Rigid wall title
(Character, maximum 100 characters)
|
|
node_ID
|
Node identifier (moving rigid wall)
(Integer)
|
|
Slide
|
Sliding flag
(Integer)
= 0: Sliding
= 1: Tied
= 2: Sliding with friction
|
|
grnd_ID1
|
Node group defining slave nodes to be added to the rigid wall
(Integer)
|
|
grnd_ID2
|
Node group defining slave nodes to be deleted from the rigid wall
(Integer)
|
|
Dsearch
|
Distance for slave search
(Real)
|
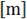
|
fric
|
Friction
(Real)
|
|
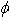
|
Diameter of the sphere
(Real)
|
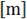
|
ffac
|
Filtering factor
Default = 0.0 (Real)
|
|
ifq
|
Filtering flag (Comments 5 through 8)
Default = 0 (Integer)
|
|
XM
|
X coordinate of M
(Real)
|
|
YM
|
Y coordinate of M
(Real)
|
|
ZM
|
Z coordinate of M
(Real)
|
|
Mass
|
Mass of the rigid wall
(Real)
|
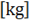
|
VX0
|
Initial velocity in X direction
(Real)
|
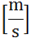
|
VY0
|
Initial velocity in Y direction
(Real)
|
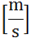
|
VZ0
|
Initial velocity in Z direction
(Real)
|
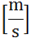
|
XM1
|
X coordinate of M1
(Real)
|
|
YM1
|
Y coordinate of M1
(Real)
|
|
ZM1
|
Z coordinate of M1
(Real)
|
|
XM2
|
X coordinate of M2
(Real)
|
|
YM2
|
Y coordinate of M2
(Real)
|
|
ZM2
|
Z coordinate of M2
(Real)
|
|
|
Type
|
Description
|
PLANE
|
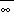 Plane Plane
|
CYL
|
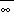 Cylinder of diameter Cylinder of diameter 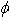
|
SPHER
|
Sphere of diameter 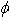
|
PARAL
|
Parallelogram
|
|
Type
|
Description
|
Sketch
|
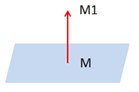
PLANE
|
MM1 defines the normal direction
|
|
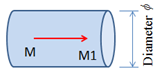
CYL
|
MM1 defines the axis of the cylinder
|
|
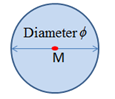
SPHER
|
M is the center of the sphere
|
|
PARAL
|
MM1 and MM2 define the parallelogram
|

|
|
| 1. | The first input defines the rigid wall coordinates of one point M or a node_ID in case of moving rigid wall. |
| 2. | The next input is the coordinate of a point M1 and possibly a point M2 (in case of a moving wall, M1 and M2 have the same motion as node_ID). |
| 3. | The slave nodes to a rigid wall can be defined as a group of nodes and/or as nodes initially at a distance less than the distance (Dsearch) from the rigid wall. |
| 4. | The friction filtering option is only available for a slide rigid wall with friction (Slide=2). |
| 5. | If ifq ≠ 0, the tangential (friction) forces in each slave node in contact are filtered using a simple rule: |
FT = 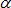 * F'T + (1 - * F'T + (1 - 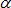 ) * F'T-1 ) * F'T-1
Where, FT is the tangential force, F'T is the tangential force at time t, F'T-1 is the tangential force at time t-1, and 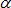 is the filtering coefficient. is the filtering coefficient.
The flag ifq defines a method for filtering, 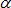 coefficient. coefficient.
| 6. | If ifq =1, filtering coefficient is directly input by you: 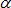 = ffac = ffac |
| 7. | If ifq =2, 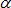 corresponds to a 3dB filtering level for user-defined frequency: corresponds to a 3dB filtering level for user-defined frequency: |
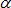 = 2 = 2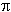 dt * freq, where dt = time step, and freq = ffac dt * freq, where dt = time step, and freq = ffac
| 8. | If ifq =3, 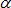 corresponds to a 3dB filtering level for user-defined frequency (frequency defined in terms of time step number): corresponds to a 3dB filtering level for user-defined frequency (frequency defined in terms of time step number): |
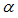 = 2 = 2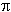 / N, with 1/freq = T = N * dt, and N = ffac / N, with 1/freq = T = N * dt, and N = ffac
| 9. | The sphere (SPHER) and parallelogram (PARAL) are not infinite. For parallelograms, the normal is defined using: |
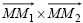
and the diameter of the sphere is definited using 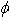 . .
| 10. | Nodal thickness of rigid wall slave nodes is not taken into account. |
|
See Also:
Implicit Features and Compatibility Information
Incompatible Kinematic Conditions in User's Guide
Rigid Wall in Theory Manual
Example 5 - Beam Frame
Example 12 - Jumping Bicycle
Example 14.1 - VPG with a Complete Finite Element Model
Example 17 - Box Beam
Example 26 - Ruptured Plate
Example 27 - Football (Soccer) Shots







