Example 27 - Football (Soccer) Shots

ex_27_football

Summary

This is mainly a demonstration example. An unusual application is used: In 1976, the European Football (Soccer) Cup final was between the Bayern of Munich and Saint Etienne. During the match, two shots from Saint Etienne rebound on the opposite bars, shaped as a square cross-section. The fact that England is the only European country not having replaced its square bars by round bars always makes French supporters believe that Saint Etienne could have won the final if the bars had been round. This example provides an answer through simulation; however, the controversy will no doubt continue.

Title

Football shot

ex_27.1

Number

27.1 Brief Description

Simulation of a football (soccer) shooting impact on bars.

Keywords

•	Q4 and T3 meshes, and Orthotropic shell

•	Airbag modeling and sensor

•	Rigid cylinder

•	Initial velocity

RADIOSS Options

•	Initial velocity (/INIVEL)

•	Initial velocities around axis (/INIVEL/AXIS)

•	Monitored volume type airbag (/MONVOL/AIRBAG1)

•	Rigid bodies (/RBODY)

•	Rigid cylinder (/RWALL)

•	Sensor (/SENSOR)

Compared to / Validation Method

•	Video films for a square cross-section case.

Input File

Bathenay’s shot: <install_directory>/demos/hwsolvers/radioss/27_Football_shots/Bathenay_circular/BAT_CIR*

<install_directory>/demos/hwsolvers/radioss/27_Football_shots/Bathenay_square/BAT_SQR*

Santini’s header: <install_directory>/demos/hwsolvers/radioss/27_Football_shots/Santini_circular/SANT_CIR*

<install_directory>/demos/hwsolvers/radioss/27_Football_shots/Santini_square/SANT_SQR*

Technical / Theoretical Level

Medium

Overview

Aim of the Problem

During the European football (Soccer) Cup final in 1976 (Bayern of Munich versus Saint Etienne), a shot from Bathenay (Fig 1) and a header from Santini (Fig 2) rebounded off the square cross-section frame of the German team’s goal. The purpose of this demonstration is to determine the influence of a square or a round cross-section bar for both cases.

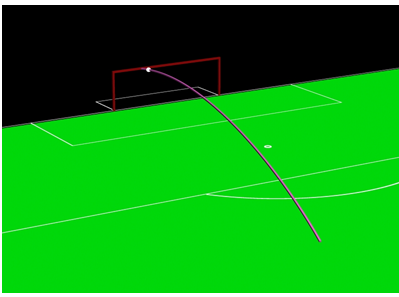
fig_27-1

Fig 1: Bathenay’s shot.

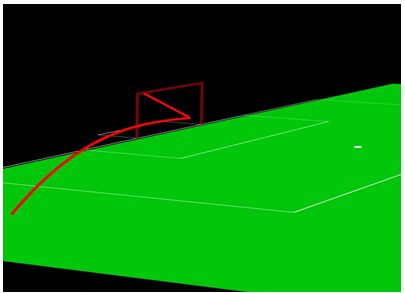
fig_27-2

Fig 2: Santini’s header

Physical Problem Description

The main differences between both shots are the incidence, the velocity and the impact point of the ball on the bar (its vertical value).

The material used for the ball follows a linear elastic orthotropic law (/MAT/LAW19) with the following characteristics:

•	Initial density: 2.01x10-3 g/mm3

•	Young modulus (dir. 1 and 2): 20000 MPa

•	Shear modulus (12, 23 and 31): 10000 MPa

•	Poisson ratio: 0.29

Units: mm, ms, g, N, MPa

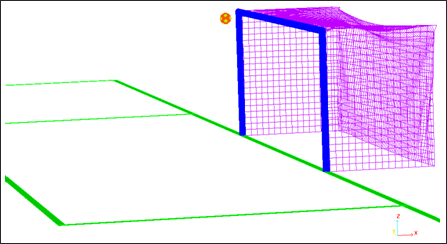
fig_27-3

Fig 3: Geometry of the problem.

Analysis, Assumptions and Modeling Description

Modeling Methodology

The ball is modeled using 60 3-node shells and 1420 4-node shells. The shell element formulations are set by default. The bar and the ground are also modeled with 4-node shell elements, but their mesh will not be used for the computation.

fig_27-4

Fig 4: Ball mesh.

RADIOSS Options Used

•	A rigid body is created, containing all the nodes of the ball. It is deactivated just before impact on the bar.

•	Two initial velocities are applied to the rigid body’s master node. They are defined using /INIVEL/AXIS for the rotary motion and /INIVEL/TRA for the translating motion.

•	The bars are modeled with a cylindrical rigid wall for the round bar and two rigid parallelograms for the square bar.

•	Gravity is taken into account using a gravity load.

•	The ball is considered as an airbag, which is activated when the rigid body is deactivated.

Simulation Results and Conclusions

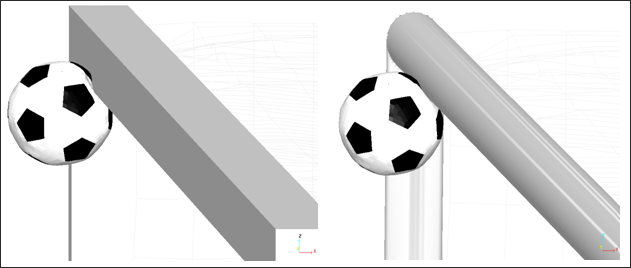
fig_27-5

Fig 5: Impact of the ball on a square and a round cross-section.

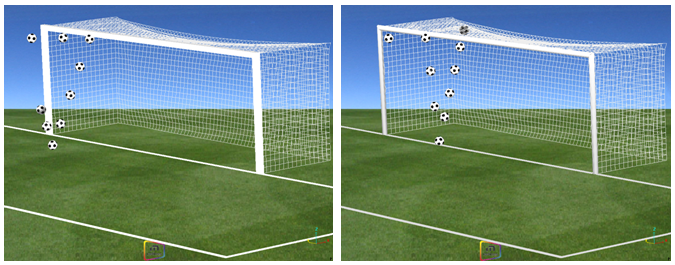
fig_27-6

Fig 6: Trajectory of the ball for Bathenay’s shot (impact on a square and a round bar respectively).

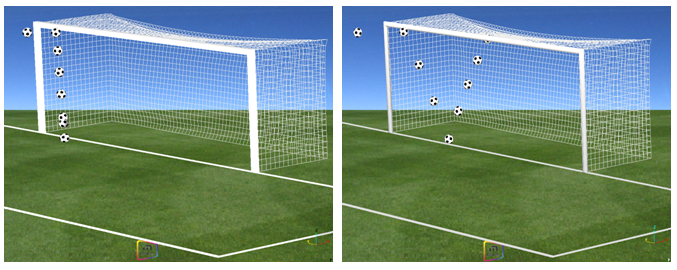
fig_27-7

Fig 7: Trajectory of the ball for Santini’s head (impact on a square and a round bar respectively).

Conclusion

Even using a simple modeling of the impact (bars modeled with rigid walls instead of parts), the simulation provides quite accurate results in the case of a square cross-section when simulations are compared to reality. The results obtained for the bars with a round cross-section show that the ball enters to the goal for both shots. However, several impact parameters, such as friction and rotational velocity are estimated as calibrating the case of a square cross-section. Conclusions on the results of the match in case of cylindrical bars should be moderated.