Example 37 - Analytical Beam |

|

|

|

|
|
Example 37 - Analytical Beam |

|

|

|

|
This example deals with the use of RADIOSS linear and nonlinear solvers. A beam submitted to a concentrated load on one extremity and fixed on the other hand is studied. This problem is well known and results can be compared with analytical solutions.
Different meshes are tested: beam, shell, thick-shell, and brick elements. For thick-shell representation, different formulations are also tested: HA8, HSEPH, and 16-node thick-shell.
Moreover, this study tests with solvers: linear and nonlinear implicit solvers, as well as nonlinear explicit solver. The linear solver is used for small displacements, whereas nonlinear can solve more problems.
The main propose of this example is to illustrate how to prepare a RADIOSS deck for linear analysis. It also demonstrates a high quality of RADIOSS finite elements to resolve linear and nonlinear problems.
TitleAnalytical beam |
|
||||||||||||||||||||
Number37.1 |
|||||||||||||||||||||
Brief DescriptionA cantilever beam submitted to a shear-bending is tested by RADIOSS linear and nonlinear solvers. Different kinds of RADIOSS finite elements provide results close to the analytical one. |
|||||||||||||||||||||
Keywords
|
|||||||||||||||||||||
RADIOSS Options
|
|||||||||||||||||||||
Compared to / Validation Method
|
|||||||||||||||||||||
Input File2 Bricks: <install_directory>/demos/hwsolvers/radioss/37_Analytical_Beam/Analytical_beam/2_bricks/explicit_nonlinear/POUTRE*
4 Bricks: <install_directory>/demos/hwsolvers/radioss/37_Analytical_Beam/Analytical_beam/4_bricks/explicit_nonlinear/POUTRE*
Beam: <install_directory>/demos/hwsolvers/radioss/37_Analytical_Beam/Analytical_beam/beam/explicit_nonlinear/POUTRE*
Shell: <install_directory>/demos/hwsolvers/radioss/37_Analytical_Beam/Analytical_beam/shell/explicit_nonlinear/POUTRE*
Thick Shell: <install_directory>/demos/hwsolvers/radioss/37_Analytical_Beam/Analytical_beam/thick_shell/explicit_nonlinear/POUTRE*
|
|||||||||||||||||||||
Technical / Theoretical LevelBeginner |
|||||||||||||||||||||
This study deals with two choices: finite element approach and resolution techniques.
A simple beam is fixed on one extremity, and loaded on the other hand by concentrated load:
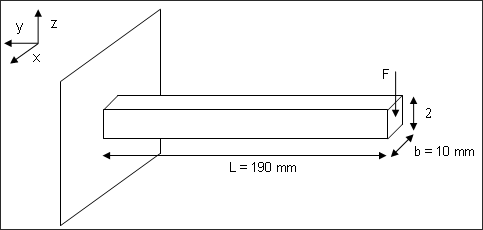
Fig 1: Geometry of the problem.
The material behavior is linear elastic law (/MAT/LAW1) with the following properties:
| • | Density: |
| • | Young modulus: E = 210 000 MPa |
| • | Poisson coefficient: |
The beam is modeled with four different kinds of mesh: beams (/BEAM), shells (/SHELL), thick-shells (/PROP/TSHELL), and bricks (/BRICK).
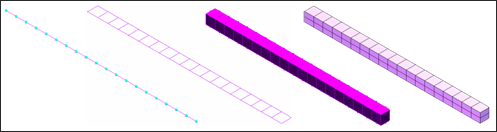
Fig 2: Different meshes.
Each formulation has particular properties (/PROP). Beam elements use the default formulation (Ismstr = 0). Furthermore, in order to satisfy Timoshenko’s beam assumptions, use the following properties:
| • | Cross section: 100 mm2 |
| • | Moment of inertia: 833.33 mm4 |
This conducts to a shell thickness of 10 mm, where BATOZ shell formulation is used (Ishell = 12).
For the solid mesh, the HA8 formulation (Isolid = 14) is applied. No reduced pressure integration is necessary for implicit computation, as the behavior is elastic (Icpre = 0).
For thick-shell elements (/PROP/TSHELL), several formulations are tested: HA8 (Isolid = 14), HSEPH (Isolid = 15), and 16-node thick-shell (Isolid = 16), which require a specific nodal connectivity, as shown below:
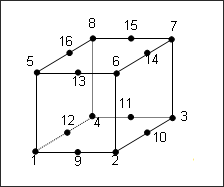
Fig 3: Thick-shell element numbering
The boundary conditions option (/BCS) is used to fix the beam on one extremity.
To apply the load, a rigid body is created (/RBODY), and then the beam is submitted to an increasing force (/CLOAD and /FUNCT).
When the loading is small enough, the beam behavior can be considered to be linear. The easiest way to resolve the problem is to use RADIOSS linear solver.
The implicit RADIOSS solver considers a static loading. It needs to define some parameters with the /IMPL option. Under the linear behavior assumption, RADIOSS linear solver can be used by putting /IMPL/LINEAR in the Engine file. The nonlinear implicit solver can be activated by /IMPL/NONLIN in the Engine file. To solve the equation, both methods need a numerical linear solver as direct solver MUMPS (/IMPL/SOLVER/2).
The nonlinear explicit solver can also be used. In this case, the load is considered to be applied dynamically. The dynamic relaxation technique (/DYREL) allows speed converge to the static solution by introducing a numerical damping. That implies the knowledge of the frequency to damp. To obtain the dominating period of the structure to damp, look at the kinetic energy variation in time during the first phase of run. The modal analysis solver by eigen values in RADIOSS can also be used.
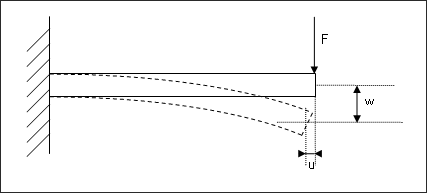
Fig 4: Notation.
For the linear problem, the analytical solution gives:
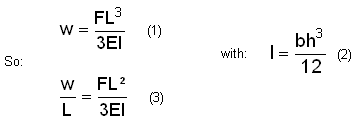
For nonlinear case, the Timoshenko and Gere study provides the following results [1]:
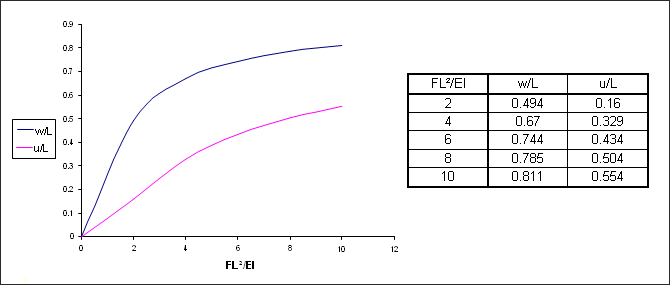
Fig 5: Timoshenko and Gere results.
In the case of linear behavior, the numerical results are quite close to the analytical solution (error lower than 0.01% for all meshes).
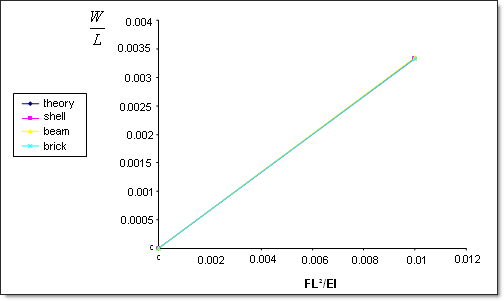
Fig 6: Linear solutions.
For the nonlinear case, the results obtained by RADIOSS with explicit and implicit solvers are in good concordance with the analytical solution of Timeshenko and Gere.
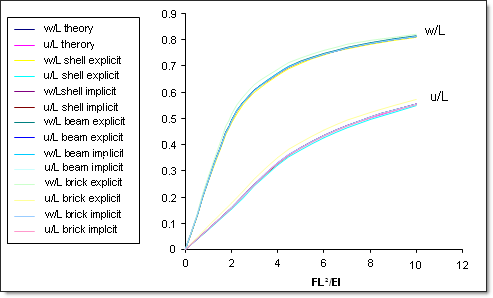
Fig 7: Comparison of results.
The numerical error or the difference between the numerical results and the analytical solution can be evaluated by:
![]() (4)
(4)
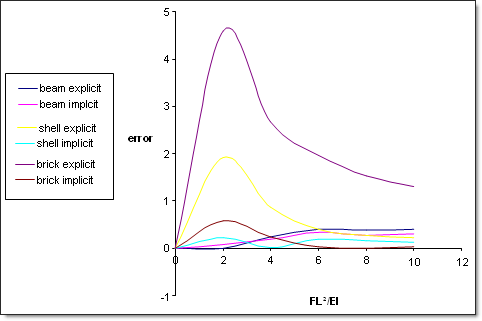
Fig 8: Error on w/L
Here it appears that errors for the slender case (![]() =2) are high for the explicit solver. This is mainly due to difficult convergence of the dynamic solution to the static response. High flexibility means low frequency vibrations and thus low efficiency of dynamic relaxation method. On the other hand, the implicit solver converges to the good solution. The error is remains lower than 0.5%.
=2) are high for the explicit solver. This is mainly due to difficult convergence of the dynamic solution to the static response. High flexibility means low frequency vibrations and thus low efficiency of dynamic relaxation method. On the other hand, the implicit solver converges to the good solution. The error is remains lower than 0.5%.
Regarding the thick-shell elements, RADIOSS results are quite close to the analytical solution. The error remains always less than 0.5%.
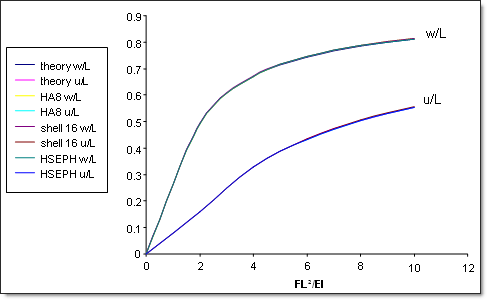
Fig 9: Thick-shell solutions.
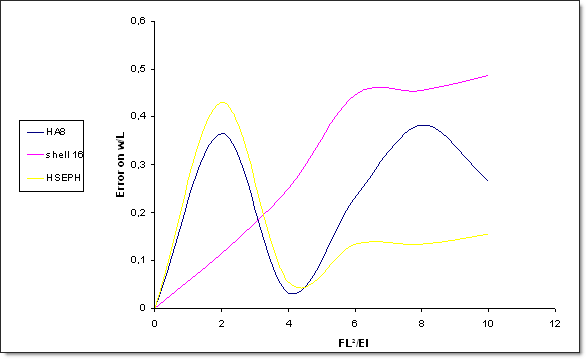
Fig 10: Error for thick-shell formulations.
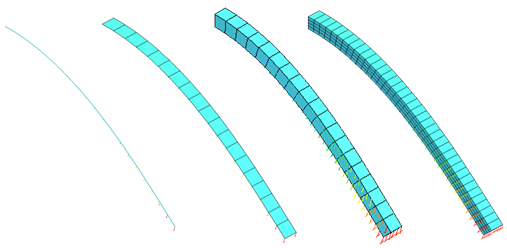
A schematic deformation mode for each case of mesh is shown in the following figures.
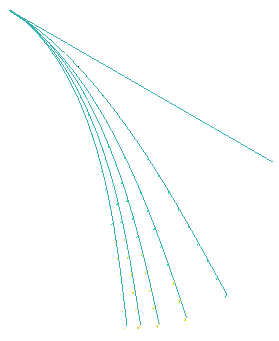
Fig 11: Beam animation
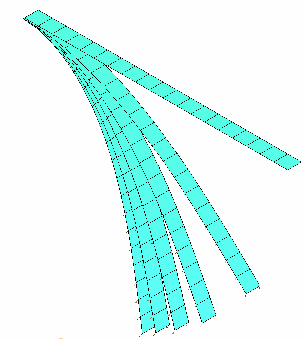
Fig 12: Shell animation.
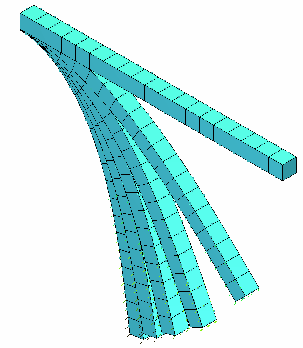
Fig 13: Shell 16 animation.
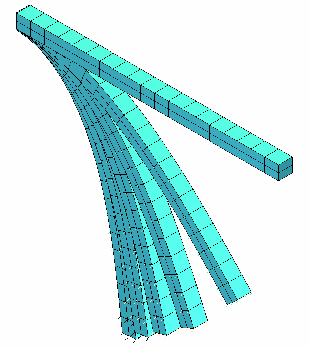
Fig 14: Brick animation
[1] S.P. Timoshenko, J.M. Gere, "Mechanics of materials", D. Van Nostrand Co, 1972