FREQ4

Bulk Data Entry

FREQ4 – Frequency List, Alternate Form 4

Description

Defines a set of frequencies for the modal method of frequency response analysis by specifying the amount of "spread" around each modal frequency and the number of equally spaced frequencies within the spread.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
FREQ4	SID	F1	F2	FSPD	NFM

Define a set of frequencies such that there will be 21 equally spaced frequencies across a frequency band of 0.7 * fN to 1.3 * fN for each modal frequency that occurs between 20 and 200.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
FREQ4	6	20.0	200.0	0.30	21

Field	Contents
SID	Set identification number. No default (Integer > 0)
F1	Lower bound of modal frequency range in cycles per unit time. Default = 0.0 (Real > 0.0)
F2	Upper bound of frequency range in cycles per unit time. Default = 1.0E20 (Real > 0.0, F2 > F1)
FSPD	Frequency spread, +/- the fractional amount specified for each mode which occurs in the frequency range F1 to F2. Default = 0.10 (1.0 > Real > 0.0)
NFM	Number of evenly spaced frequencies per "spread" mode. Default = 3 (Integer > 0; If NFM is even, NFM + 1 will be used)

Comments

1.	FREQ4 applies only to the modal method of frequency response analysis.

2.	FREQ4 entries must be selected in the Subcase Information section with FREQUENCY = SID.

3.	There will be NFM excitation frequencies between and , for each modal frequency in the range F1 to F2. If this computation results in excitation frequencies less than F1 and greater than F2, those computed excitation frequencies are ignored.

Excitation frequencies may be based on modal frequencies that are not within the range (F1 and F2) as long as the calculated excitation frequencies are within the range. Similarly, an excitation frequency calculated based on natural frequencies within the range (F1 through F2) may be excluded if it falls outside the range.

5.	The frequency spread can be used also to define the half-power bandwidth. The half-power bandwidth is given by , where, is the damping ratio. Therefore, if FSPD is specified equal to the damping ratio for the mode, NFM specifies the number of excitation frequencies within the half-power bandwidth.

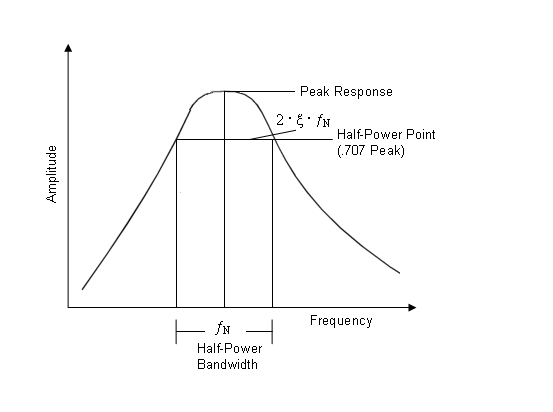
freq4_2_w_curve

6.	Since the forcing frequencies are near structural resonances, it is important that some amount of damping be specified.

7.	All FREQi entries with the same set identification numbers will be used. Duplicate frequencies will be ignored. fN and fN-1 are considered duplicated if:

where, DFREQ is a user parameter, with a default of 10-5. The values fMAX and fMIN are the maximum and minimum excitation frequencies of the combined FREQi entries.

8.	In design optimization, the excitation frequencies are derived from the modal frequencies computed at each design iteration.

9.	In modal analysis, solutions for modal degrees-of-freedom from rigid body modes at zero excitation frequencies may be discarded. Solutions for non-zero modes are retained.

10.	This card is represented as a loadcollector in HyperMesh.